中文 | English

1. Overview

The Transformer model is relatively complex. Many people, myself included, may have studied it but still don't know how to use it.

This guide approaches the Transformer as a "black box" and provides a practical guide to using PyTorch's nn.Transformer.

This guide covers the following:

• Explanation of the Transformer training process
• Explanation of the Transformer inference process
• Explanation of the Transformer’s inputs and outputs
• Detailed explanation of each parameter in nn.Transformer
• In-depth look at the masking mechanism in nn.Transformer
• Practical example: training a simple copy task using nn.Transformer

You can find the source code for this guide in this project.

Before we begin, let’s import the necessary packages:

```python
import math
import random

import torch
import torch.nn as nn
```

2. Viewing the Transformer as a Black Box

Below is a classic diagram of the Transformer model:

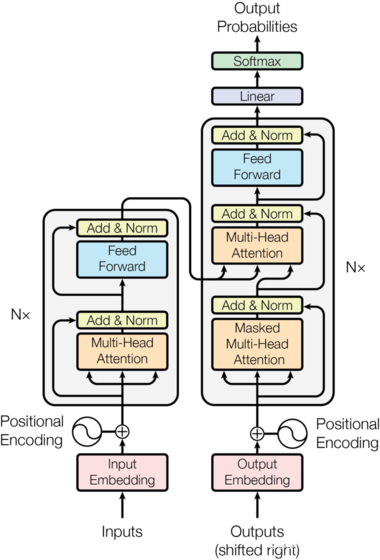
Let’s simplify things by treating it as a black box:

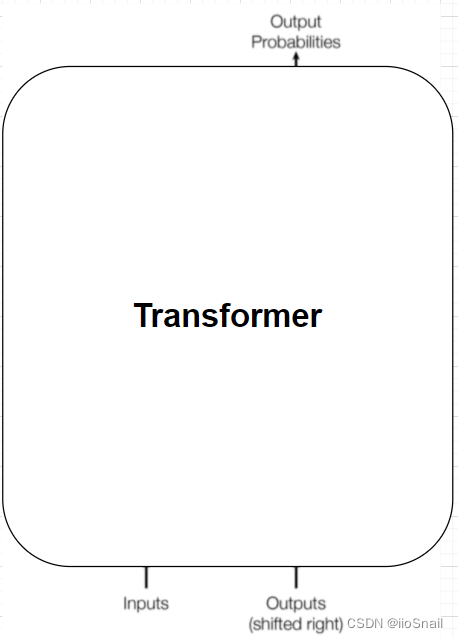
Now, let’s look at the inputs and outputs of the Transformer:

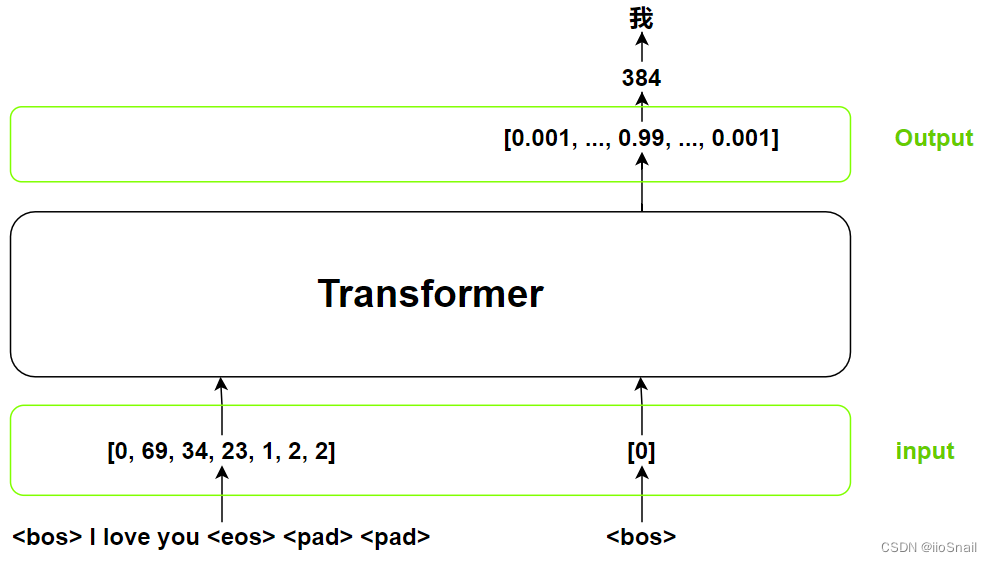
"我" is a Chinese character which means "I".

Here, we have an example of a translation task with the Transformer’s inputs and outputs. The inputs consist of two main parts:

• Inputs: All the tokens of the sentence you want to translate. Typically, tokens include markers like <bos>(beginning of sentence), <eos>(end of sentence) and <pad>(padding). Padding is used to standardize sentence length within a batch. Programmers usually name this variable as src.
• Outputs (shifted right): This is the output from the previous step. Initially, it starts with <bos>. For example, after predicting the first token "我", the next input(outputs (shifted right)) would be <bos> 我. This variable is often named tgt.

The Transformer's output is a probability distribution that indicates which token is most likely to be the result.

3. The Inference Process of the Transformer

Let's start with the Transformer's inference process since it's straightforward. Based on the previous explanation, you might already have a general understanding.

In the previous chapter, we mentioned the first step of Transformer inference. Here is the second step, shown in the diagram:

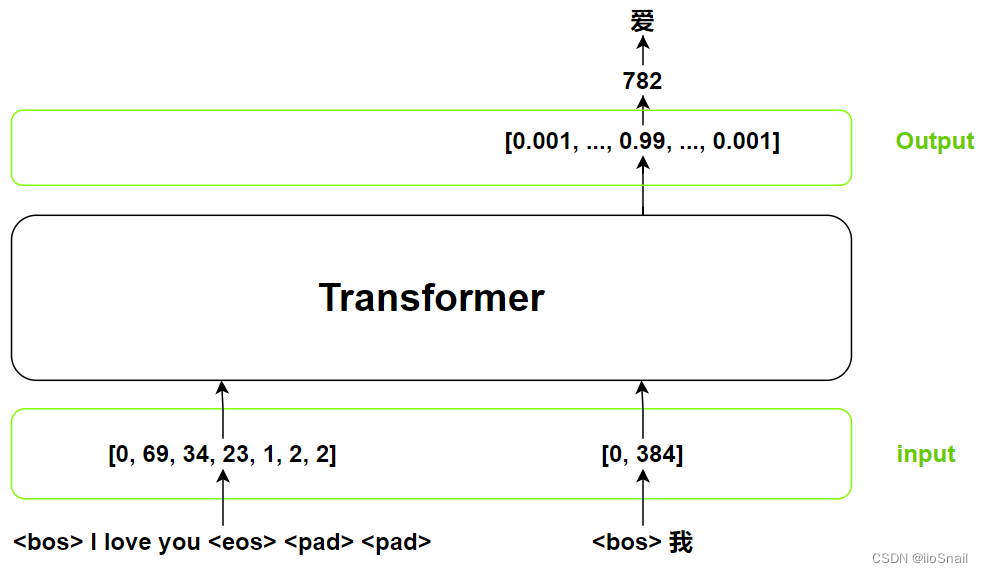
"爱" means "love"

In the inference process, the Transformer is repeatedly called until it outputs <eos> (end of sequence) or reaches the maximum sentence length.

In practice, the Transformer’s Encoder typically only runs once during inference. However, for simplicity, here we demonstrate it as if the entire model re-runs each step.

4. The Training Process of the Transformer

During inference, we output one word at a time, but doing this in training would be inefficient. Instead, we give the entire target sequence to the Transformer in one go. The diagram below illustrates this:

From the diagram, we can see the main similarities and differences between the Transformer’s training and inference processes:

• Same Source Input (src) : The Transformer’s input part (src parameter) is the same in both cases, representing the sentence to be translated.
• Different Target Input (tgt) : In inference, the target (tgt) begins with <bos> and appends each previous output (e.g., the second input is <bos> 我). In training, however, we provide the entire “complete” result in one pass to the Transformer. This approach is effectively the same as adding tokens one by one (for more details, see the Mask Attention in this post). Another detail is that the target (tgt) is one token shorter than the source (src). For example, if we want to predict <bos> 我 爱 你 <eos> (ignoring padding), the last input parameter tgt will be <bos> 我 爱 你 (without <eos>). This is because the prediction process stops if the output token is <eos>. Therefore, when processing tgt, the final token is usually removed. Note: In most sentences within a batch, the final token is <pad>.
• More Outputs: In training, the Transformer produces multiple probability distributions at once. For example, in the diagram, 我 corresponds to the output when tgt is <bos>, 爱 corresponds to <bos> 我, and so forth. Once we get the output distributions, we can compute the loss directly, without converting these distributions back into words. Note that here, our output length is six, which corresponds to the tokens 我 爱 你 <eos> <pad> <pad>, excluding <bos> (because we don’t predict this token). When calculating the loss, we only use these tokens as the labels, excluding <bos>. The variable of the labels is often named tgt_y.

After obtaining the Transformer outputs, we can calculate the loss, as illustrated in the following diagram:

5. nn.Transformer in Pytorch

5.1 Overview of nn.Transformer

PyTorch provides a out-of-the-box implementation of the Transformer model, so we can directly use it. However, there are some differences between nn.Transformer and the typical Transformer model structure, as illustrated here:

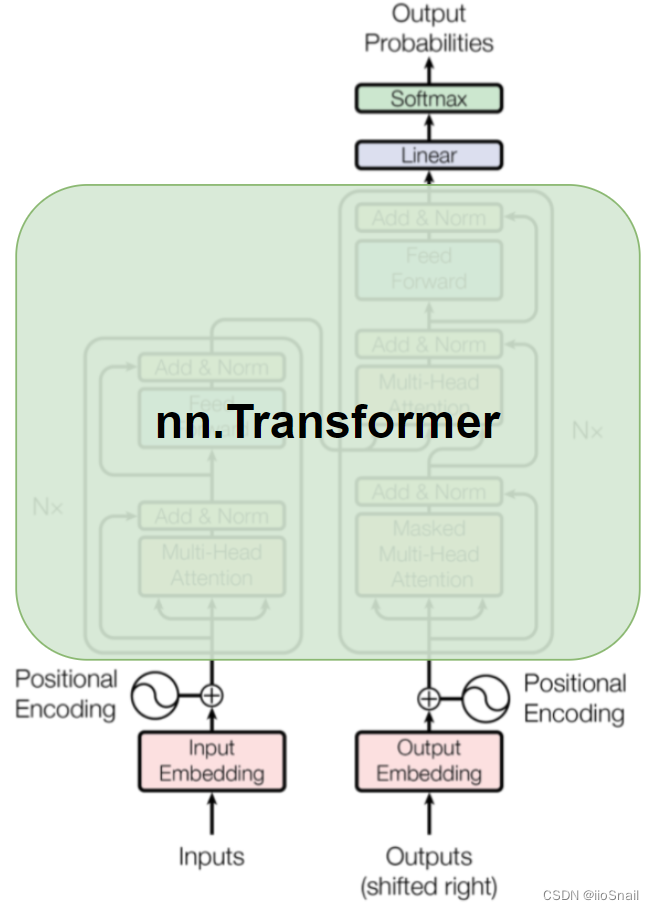
The PyTorch nn.Transformer doesn't include the Embedding, Positional Encoding, and final Linear+Softmax layers, so let’s briefly go over these parts:

• Embedding: The embedding layer is used for mapping tokens to high-dimensional vectors. (e.g., mapping the token "123" to [0.34, 0.45, 0.123, ..., 0.33]). Pytorch provides an implementation of an embedding layer called nn.Embedding. It’s important to note that the parameters of nn.Embedding aren't fixed—they also participate in gradient descent.
• Positional Encoding: This is used for adding positional information to token encodings. For example, in the sentence "I love you", the encoded vectors don't inherently include position information (like "love" being between "I" and "you"). Positional Encoding provides this context information, and the difference it makes can be quite significant.
• Linear+Softmax: A linear layer and a Softmax function, used for token prediction from the transformer's output.

Let's quickly demonstrate the basic use of nn.Transformer:

```python
# Define an encoder with a vocabulary size of 10, encoding tokens into 128-dimensional vectors
embedding = nn.Embedding(10, 128)
# Define the transformer with a model dimension of 128 (matching the token vector dimension)
transformer = nn.Transformer(d_model=128, batch_first=True) # Remember to set batch_first to true.
# Define the source sentence, e.g., <bos> I love to eat meat and vegetables <eos> <pad> <pad>
src = torch.LongTensor([[0, 3, 4, 5, 6, 7, 8, 1, 2, 2]])
# Define the target sentence, e.g., <bos> I like to eat meat and vegetables <eos> <pad>
tgt = torch.LongTensor([[0, 3, 4, 5, 6, 7, 8, 1, 2]])
# Pass the token encodings to the transformer (Positional Encoding omitted for simplicity here)
outputs = transformer(embedding(src), embedding(tgt))
outputs.size()
```

```
torch.Size([1, 9, 128])
```

The output shape from the transformer matches the encoded shape of tgt. In training, we pass all transformer outputs to the final Linear layer, while in inference, we only pass the final token of the output (outputs[:, -1]) to Linear.

5.2 nn.Transformer Construction Parameters

The Transformer model has a variety of parameters, so let's open up the "black box" a little:

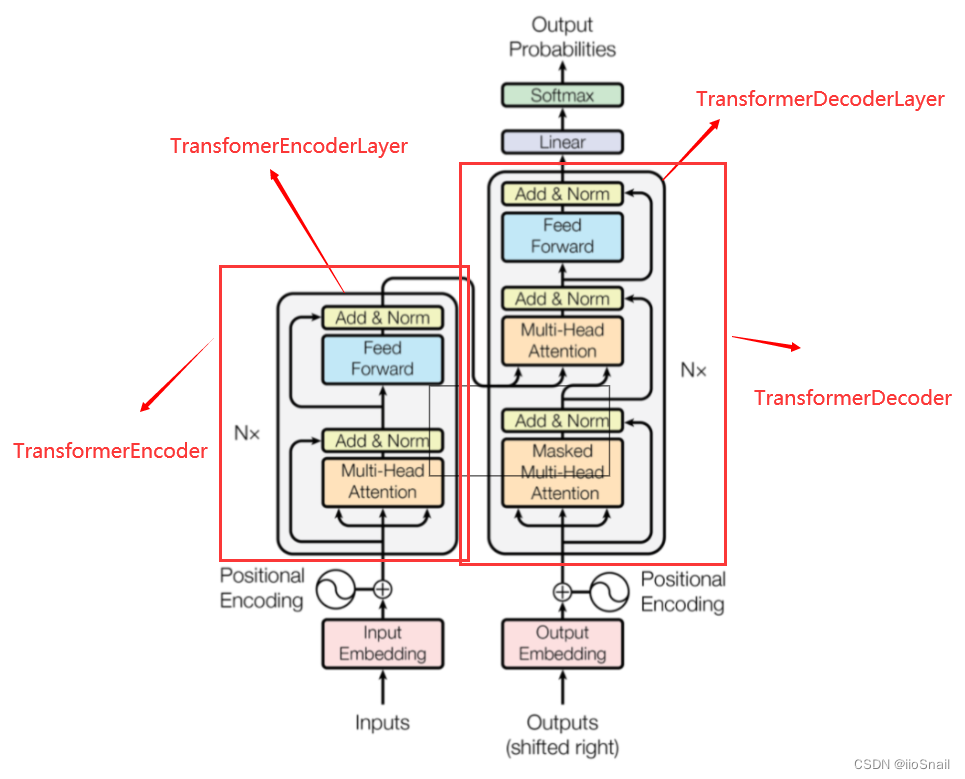
The nn.Transformer module consists of two main components: nn.TransformerEncoder and nn.TransformerDecoder. nn.TransformerEncoder is built by stacking multiple nn.TransformerEncoderLayers, where Nx in the figure represents the number of stacked layers. Similarly, nn.TransformerDecoder is constructed with multiple nn.TransformerDecoderLayers.

Below are the construction parameters for nn.Transformer:

• d_model: The feature dimension of input parameters for the Encoder and Decoder, which represents the word vector dimension. Default is 512.
• nhead: The number of heads in the multi-head attention mechanism. For more on Attention mechanisms, see this article. Note that this value doesn’t affect network depth or parameter count. Default is 8. Note that this value doesn’t affect network depth or parameter count. Default is 8.
• num_encoder_layers: The number of nn.TransformerEncoderLayer. Increasing this makes the network deeper, with more parameters and higher computational cost. Default is 6.
• num_decoder_layers: The number of nn.TransformerDecoderLayer, which similarly affects depth and computational load. Default is 6.
• dim_feedforward: The number of neurons in the hidden layer of the Feed Forward network (the fully connected layer following Attention). Higher values increase parameter count and computation. Default is 2048.
• dropout: The dropout rate. Default is 0.1.
• activation: The activation function for the Feed Forward layer. Options are relu or gelu as strings, or any callable function. Default is relu.
• custom_encoder: Allows custom Encoder. If you prefer not to use the default nn.TransformerEncoder, you can implement your own. Default is None.
• custom_decoder: Allows custom Decoder. Similar to the encoder, you can implement your own if needed. Default is None.
• layer_norm_eps: The eps parameter value for BatchNorm in the Add&Norm layer. Default is 1e-5.
• batch_first: Determines if the batch dimension is the first dimension. If batch_first=True, input shape should be (batch_size, sequence_length, embedding_dim) ; Or else, it should be (sequence_length, batch_size, embedding_dim) ; Default is False. Note: Many users expect batch size to be the first dimension, so this parameter may be set to True to avoid errors.
• norm_first: Controls whether normalization is applied first. In the diagram, the default order is Attention -> Add -> Norm; if set to True, the order switches to Norm -> Attention -> Add.

5.3 nn.Transformer.forward Parameters

The forward parameters in a Transformer require a thorough explanation. I'll provide basic descriptions briefly here and give a detailed breakdown of each one in later chapters:

• src: The input for the Encoder. It’s the tensor after token embedding and positional encoding. Required. Shape is: (batch_size, number_of_words, embedding_dimension).
• tgt: Similar to src, but it’s the input for the Decoder. Required. Shape is: (number_of_words, embedding_dimension)
• src_mask: Mask for the src input. Rarely used. Shape is: (number_of_words, number_of_words).
• tgt_mask: Mask for the tgt input. Commonly used. Shape is: (number_of_words, number_of_words)
• memory_mask: Mask for the Encoder's output memory. Rarely used. Shape is: (batch_size, number_of_words, number_of_words).
• src_key_padding_mask: Mask applied to the tokens in src. Commonly used. Shape is: (batch_size, number_of_words)
• tgt_key_padding_mask: Mask applied to the tokens in tgt. Commonly used. Shape is: (batch_size, number of words)
• memory_key_padding_mask: Mask for memory keys. Rarely used. Shape is: (batch_size, number_of_words)

Note: In pytorch code, False indicates "no mask" and True indicates "mask". If you find your output includes nan, please check if you confused the True/False. Furthermore, src_mask, tgt_mask, and memory_mask don’t require batch dimensions.

5.3.1 src and tgt

The src and tgt parameters represent the inputs to the Encoder and Decoder, respectively. These are the result of embedding + positional encoding.

For example, suppose our initial input is [[0, 3, 4, 5, 6, 7, 8, 1, 2, 2]] with a shape of (1, 10), meaning there is one sentence (batch_size=1), and the sentence consists of 10 tokens.

After passing this through the embedding layer (including positional encoder), the shape changes to (1, 10, 128), where each of the 10 tokens is now represented as a 128-dimensional vector.

The src parameter refers to this (1, 10, 128) tensor. The tgt parameter works in the same way for the target sequence.

5.3.2 src_mask, tgt_mask and memory_mask

To truly understand the mask theory, you need some familiarity with the Attention mechanism. For a detailed explanation, you can refer to this article. Below is a brief overview.

In the Attention layer, each token is enriched with contextual information, meaning that every token gains additional meaning by incorporating information from other tokens in the sequence. For instance: In the sentences "Apples are tasty" and "Apple iPhone is fun", the word "apple" refers to different things depending on the context provided by "tasty" or "iPhone."

The Attention mechanism enables this context-awareness by constructing a matrix that represents the relationships between all tokens. For example:

```
       Apples are tasty
Apples [[0.5, 0.1, 0.4],
are     [0.1, 0.8, 0.1],
tasty   [0.3, 0.1, 0.6],]
```

In this matrix, the first row [0.5, 0.1, 0.4] shows the relationship between "Apples" and itself, "are," and "tasty." Using this matrix, we can create a context-enriched representation of "Apple" as:

$$\begin{array}{r}{\text{Apples}}^{\prime }=\text{Apples}\times 0.5+\text{are}\times 0.1+\text{tasty}\times 0.4\end{array}$$

However, during inference (sequence generation), tokens are generated one by one. If "Apples are tasty" is the target (tgt), the word "Apples" should not have access to the future tokens "are" and "tasty." Instead, we want:

$$\begin{array}{r}{\text{Apples}}^{\prime }=\text{Apples}\times 0.5\end{array}$$

Similarly, the token "are" can include information from "Apple," but not from "tasty." So, we expect:

$$\begin{array}{r}{\text{are}}^{\prime }=\text{Apples}\times 0.1+\text{are}\times 0.8\end{array}$$

To enforce this restriction, we modify the attention matrix:

```
       Apples are tasty
Apples [[0.5, 0,   0],
are     [0.1, 0.8, 0],
tasty   [0.3, 0.1, 0.6]]
```

This is where masks come in. Masks allow us to selectively "hide" future tokens during computation. For the example above, the mask would look like this:

```
       Apples   are  tasty
Apples [[ 0,  -inf, -inf],
are     [ 0,   0,   -inf],
tasty   [ 0,   0,    0]]
```

Here:

• 0 means the token is visible (not masked).
• -inf means the token is masked (invisible). This works because applying softmax to -inf results in a probability of 0.

For the target mask (tgt_mask), we generate a triangular mask that prevents tokens from attending to future tokens. This can be achieved using PyTorch's nn.Transformer.generate_square_subsequent_mask method:

```python
nn.Transformer.generate_square_subsequent_mask(5) # '5' refers to the number of tokens in the target sequence
```

```
tensor([[0., -inf, -inf, -inf, -inf],
        [0., 0., -inf, -inf, -inf],
        [0., 0., 0., -inf, -inf],
        [0., 0., 0., 0., -inf],
        [0., 0., 0., 0., 0.]])
```

Based on the above analysis, src and memory typically don't require masking, making it an infrequent operation.

5.3.3 key_padding_mask

In both our src and tgt sequences, apart from the main tokens, there are three special tokens: <bos>, <eos>, and <pad>. Among these, <pad> is purely used for padding purposes to standardize sequence lengths within a batch. This token has no inherent meaning, so we want to exclude it from participating in the attention calculations by masking it. This is where the key_padding_mask parameter comes in.

For instance, suppose our src sequence is [[0, 3, 4, 5, 6, 7, 8, 1, 2, 2]], where 2 represents <pad>. The corresponding src_key_padding_mask would look like [[0, 0, 0, 0, 0, 0, 0, 0, -inf, -inf]], effectively masking the two <pad> tokens at the end.

The same logic applies to tgt_key_padding_mask. However, memory_key_padding_mask is generally unnecessary and can be skipped.

In many Transformer implementations, including the official PyTorch code, tgt_mask and tgt_key_padding_mask are often combined into one parameter. For example:

```
[[0., -inf, -inf, -inf],  # tgt_mask
 [0., 0., -inf, -inf],
 [0., 0., 0., -inf],
 [0., 0., 0., 0.]]
 +
 [[0., 0., 0., -inf]]  # tgt_key_padding_mask
 =
[[0., -inf, -inf, -inf],  # Merge them into one matrix
 [0., 0., -inf, -inf],
 [0., 0., 0., -inf],
 [0., 0., 0., -inf]]
```

5.4 Using nn.Transformer

Now, let's walk through a simple example of how to use PyTorch's nn.Transformer.

Step 1: Define src and tgt sequences

```python
src = torch.LongTensor([
    [0, 8, 3, 5, 5, 9, 6, 1, 2, 2, 2],
    [0, 6, 6, 8, 9, 1 ,2, 2, 2, 2, 2],
])
tgt = torch.LongTensor([
    [0, 8, 3, 5, 5, 9, 6, 1, 2, 2],
    [0, 6, 6, 8, 9, 1 ,2, 2, 2, 2],
])
```

Step 2: Define a helper function to generate src_key_padding_mask and tgt_key_padding_mask

```python
def get_key_padding_mask(tokens):
    key_padding_mask = torch.zeros(tokens.size())
    key_padding_mask[tokens == 2] = -torch.inf
    return key_padding_mask

src_key_padding_mask = get_key_padding_mask(src)
tgt_key_padding_mask = get_key_padding_mask(tgt)
print(tgt_key_padding_mask)
```

```
tensor([[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
        [0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf]])
```

Step 3: Generate the tgt_mask using the Transformer utilities

```python
tgt_mask = nn.Transformer.generate_square_subsequent_mask(tgt.size(-1))
print(tgt_mask)
```

```
tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
        [0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
        [0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
```

Step 4: Define embeddings and the Transformer model

```python
# Define the embedding layer (vocabulary size = 10, embedding size = 128)
embedding = nn.Embedding(10, 128)

# Define the Transformer model (hidden dimension = 128, consistent with embedding size)
transformer = nn.Transformer(d_model=128, batch_first=True)  # Ensure batch dimension is first

# Pass the embedded tokens into the Transformer (without positional encoding for now)
outputs = transformer(
    embedding(src),
    embedding(tgt),
    tgt_mask=tgt_mask,
    src_key_padding_mask=src_key_padding_mask,
    tgt_key_padding_mask=tgt_key_padding_mask
)

# Print the output tensor size
print(outputs.size())
```

```
torch.Size([2, 10, 128])
```

6. Practice: Implementing a Simple Copy Task Using nn.Transformer

Task Description: The goal is to use a Transformer to predict the input itself. For example, given the input [0, 3, 4, 6, 7, 1, 2, 2], the expected output is [0, 3, 4, 6, 7, 1].

Define the Maximum Sequence Length

```python
max_length=16
```

Create the Positional Encoding Class. You don’t need to worry about the details of how it works; you can directly use this implementation. Here's the code:

```python
class PositionalEncoding(nn.Module):
    "Implement the Positional Encoding function."

    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Initialize the positional encoding tensor with shape (max_len, d_model)
        pe = torch.zeros(max_len, d_model)
        # Create a tensor of positions: [[0], [1], [2], ..., [max_len-1]]
        position = torch.arange(0, max_len).unsqueeze(1)
        # Compute the scaling factor for sine and cosine functions
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
        )
        # Compute positional encodings for even indices (2i)
        pe[:, 0::2] = torch.sin(position * div_term)
        # Compute positional encodings for odd indices (2i+1)
        pe[:, 1::2] = torch.cos(position * div_term)
        # Add a batch dimension to the positional encoding tensor
        pe = pe.unsqueeze(0)
        # Register `pe` as a buffer (not trainable but saved with the model)
        self.register_buffer("pe", pe)

    def forward(self, x):
        """
        Input:
        - x: Embedded inputs with shape (batch_size, seq_len, embedding_dim), e.g., (1, 7, 128).

        Output:
        - The input combined with positional encodings.
        """
        # Add the positional encoding to the input embeddings
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        return self.dropout(x)
```

Defining Our Copy Model

```python
class CopyTaskModel(nn.Module):

    def __init__(self, d_model=128):
        super(CopyTaskModel, self).__init__()

        # Define the embedding layer with a vocabulary size of 10.
        # Note: For simplicity, we’re not predicting numbers with decimal points.
        self.embedding = nn.Embedding(num_embeddings=10, embedding_dim=128)

        # Define the Transformer model. The hyperparameters are arbitrarily chosen.
        self.transformer = nn.Transformer(d_model=128, num_encoder_layers=2, num_decoder_layers=2, dim_feedforward=512, batch_first=True)

        # Define the positional encoding layer
        self.positional_encoding = PositionalEncoding(d_model, dropout=0)

        # Define the final linear layer. We’re skipping Softmax here since it’s not needed.
        # CrossEntropyLoss, used later, inherently applies Softmax.
        self.predictor = nn.Linear(128, 10)

    def forward(self, src, tgt):
        # Generate masks
        tgt_mask = nn.Transformer.generate_square_subsequent_mask(tgt.size()[-1])
        src_key_padding_mask = CopyTaskModel.get_key_padding_mask(src)
        tgt_key_padding_mask = CopyTaskModel.get_key_padding_mask(tgt)

        # Encode the source (src) and target (tgt) inputs
        src = self.embedding(src)
        tgt = self.embedding(tgt)

        # Add positional information to the tokens in src and tgt
        src = self.positional_encoding(src)
        tgt = self.positional_encoding(tgt)

        # Pass the prepared data into the Transformer
        out = self.transformer(src, tgt,
                               tgt_mask=tgt_mask,
                               src_key_padding_mask=src_key_padding_mask,
                               tgt_key_padding_mask=tgt_key_padding_mask)

        """
        Here, we directly return the output of the Transformer.
        The behavior during training and inference is different, 
        so we apply the linear layer for predictions outside of this model.
        """
        return out

    @staticmethod
    def get_key_padding_mask(tokens):
        """
        Generate the key padding mask for the input tokens.
        """
        key_padding_mask = torch.zeros(tokens.size())
        key_padding_mask[tokens == 2] = -torch.inf
        return key_padding_mask

```

```python
model = CopyTaskModel()
```

Let's simply try our Transformer model:

```python
src = torch.LongTensor([[0, 3, 4, 5, 6, 1, 2, 2]])
tgt = torch.LongTensor([[3, 4, 5, 6, 1, 2, 2]])
out = model(src, tgt)
print(out.size())
print(out)
```

```
torch.Size([1, 7, 128])
tensor([[[ 2.1870e-01,  1.3451e-01,  7.4523e-01, -1.1865e+00, -9.1054e-01,
           6.0285e-01,  8.3666e-02,  5.3425e-01,  2.2247e-01, -3.6559e-01,
          .... 
          -9.1266e-01,  1.7342e-01, -5.7250e-02,  7.1583e-02,  7.0782e-01,
          -3.5137e-01,  5.1000e-01, -4.7047e-01]]],
       grad_fn=<NativeLayerNormBackward0>)
```

Defining the Loss Function and Optimizer: Since this is a multi-class classification task, we’ll use CrossEntropyLoss as our loss function.

```python
criteria = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=3e-4)
```

Next, let’s define a utility function that generates random batches of data:

```python
def generate_random_batch(batch_size, max_length=16):
    src = []
    for i in range(batch_size):
        # Randomly determine the sentence length
        random_len = random.randint(1, max_length - 2)
        # Generate random tokens, adding <bos> at the start and <eos> at the end
        random_nums = [0] + [random.randint(3, 9) for _ in range(random_len)] + [1]
        # Pad the sequence to the maximum length
        random_nums = random_nums + [2] * (max_length - random_len - 2)
        src.append(random_nums)
    src = torch.LongTensor(src)
    # tgt excludes the last token
    tgt = src[:, :-1]
    # tgt_y excludes the first token
    tgt_y = src[:, 1:]
    # Calculate the number of valid tokens in tgt_y (i.e., tokens that are not <pad>)
    n_tokens = (tgt_y != 2).sum()

    # n_tokens is the total count of valid tokens in tgt_y, which will be used for loss normalization
    return src, tgt, tgt_y, n_tokens
```

```python
generate_random_batch(batch_size=2, max_length=6)
```

```
(tensor([[0, 7, 6, 8, 7, 1],
         [0, 9, 4, 1, 2, 2]]),
 tensor([[0, 7, 6, 8, 7],
         [0, 9, 4, 1, 2]]),
 tensor([[7, 6, 8, 7, 1],
         [9, 4, 1, 2, 2]]),
 tensor(8))
```

let's train the Model:

```python
total_loss = 0

for step in range(2000):
    # Generate a batch of random data
    src, tgt, tgt_y, n_tokens = generate_random_batch(batch_size=2, max_length=max_length)

    # Reset gradients
    optimizer.zero_grad()
    # Pass the input through the transformer model
    out = model(src, tgt)
    # Feed the output through the final linear layer for predictions
    out = model.predictor(out)
    """
    Compute the loss. During training, predictions are made for all output tokens,
    so we need to reshape `out`:
        The shape of `out` is (batch_size, sequence_length, vocab_size), which we
        reshape into (batch_size * sequence_length, vocab_size).
    Among these predictions, we only calculate the loss for non-<pad> tokens,
    so we normalize the loss by dividing it by n_tokens.
    """
    loss = criteria(out.contiguous().view(-1, out.size(-1)), tgt_y.contiguous().view(-1)) / n_tokens
    # Backpropagate the loss
    loss.backward()
    # Update model parameters
    optimizer.step()

    total_loss += loss

    # Print the loss every 40 steps
    if step != 0 and step % 40 == 0:
        print("Step {}, total_loss: {}".format(step, total_loss))
        total_loss = 0

```

```
Step 40, total_loss: 3.570814609527588
Step 80, total_loss: 2.4842987060546875
...
Step 1920, total_loss: 0.4518987536430359
Step 1960, total_loss: 0.37290623784065247
```

Once the model is trained, we can test it to see how well it performs:

```python
model = model.eval()
# Define a sample input `src`
src = torch.LongTensor([[0, 4, 3, 4, 6, 8, 9, 9, 8, 1, 2, 2]])
# Start the `tgt` sequence with <bos> and check if the model can reproduce the values from `src`
tgt = torch.LongTensor([[0]])
```

```python
# Predict one token at a time until <eos> is generated or the maximum sequence length is reached
for i in range(max_length):
    # Pass the input through the transformer
    out = model(src, tgt)
    # Get the prediction for the last token (only need the last word of the output sequence)
    predict = model.predictor(out[:, -1])
    # Find the index of the highest probability token
    y = torch.argmax(predict, dim=1)
    # Concatenate the predicted token with the previous sequence
    tgt = torch.concat([tgt, y.unsqueeze(0)], dim=1)

    # Stop the loop if <eos> is predicted
    if y == 1:
        break
print(tgt)
```

```
tensor([[0, 4, 3, 4, 6, 8, 9, 9, 8, 1]])
```

As shown above, the model successfully predicted the original input src.

---

References

nn.Transformer Official Documentation: https://pytorch.org/docs/stable/generated/torch.nn.Transformer.html

In-Depth Breakdown of Self-Attention, Multi-Head and Masked Attention: https://iiosnail.blogspot.com/2024/11/attention-en-01.html