小样本学习（Few-shot Learning）入门

iioSnail
18 Oct, 2024

中文 | English

基本概念

小样本学习（few-shot learning）是什么：就是使用很少的样本来进行分类或回归

Few-shot Learning的目标：让机器学会自己学习

小样本学习的直观理解：

① 前提：首先要知道，训练一个模型的目的不是为了让模型如何分辨大象和蚂蚁，而是让模型具有判断图片“异同”的能力，即让模型看到两张图片后，它能分别出这俩是不是一个类别。这样，当我们在用大数据集训练出一个分类器后，在测试阶段给模型一个从来没见过的类别的图片（假设给了一个水獭图片），此时模型虽然不知道它是什么类别，但是依然能知道它不属于之前的所有类别。这时如果再给一个相同类别的图片（假设又给了一张水獭图片），此时虽然模型从来没见过这种类别的图片（模型从来没见过水獭），但模型依然能知道这俩是一种类别（模型能判断出这两张图片是一种动物） ② 思路：先用大的训练数据集训练出一个具备判断“异同”能力的模型，在测试阶段，再给一个小样本数据集（称为Support Set），里面会包含模型没见过的样本类别，然后让模型判断当前给的图片属于 Support Set 中的哪一个类别。

例如：


在这里插入图片描述
上图中，假设目前有一个训练好的图片分类器，但是该模型没见过水獭（otter），此时测试阶段希望模型可以分辨水獭，这样就可以给模型一个support set，让它从这里面选，query的图片是support set中的哪一种

Few-shot learning 是 Meta Learning 的 一种，Meta Leanring 就是去学习如何学习（Learn to learn）

k-way n-shot support Set：Support Set 就是帮助模型去分辨新类别的小样本数据集。$k$ 代表小样本中类别的数量，$n$ 代表每个类别有多少数据。例如，有3个类别，每个类别只有一个样本，那么就是 3-way one-shot.

  • k-way: k 的数量越多，分类准确率越低
  • n-shot: n 的数量越多，分类准确率越高

Few-shot Learning的基本思路（Basic Idea）： 学习一个相似度函数（similarity function）：$\text{sim}(x, x')$ ，来判别样本 $x$ 与 $x'$ 的相似度，相似度越高，表示这两个样本越可能是同一个类别。例如，可以通过一个很大的数据集学习出一个相似度函数，然后用该函数进行预测。

这里的相似度函数指的是整个模型。

孪生网络（Siamese Network）

Siamese Network 是一种用于小样本学习的网络

该网络所用训练数据集（Training Data）包含两部分：

  1. 正样本（Positive Samples ）：两个“同类别”的样本构成的样本对 $(x_i, x_j, 1)$， 其中 1 表示 $x_i$ 和 $x_j$ 是同一个类别的样本，例如：$(老虎a, 老虎a, 1)$
  2. 负样本（Negative Samples）：两个“不同类别”的样本构成的样本对$(x_i, x_j, 0)$，其中 0 表示 $x_i$ 和 $x_j$ 不是同一个类别的样本，例如 $(汽车a, 大象a, 0)$

Siamese Network的网络结构：


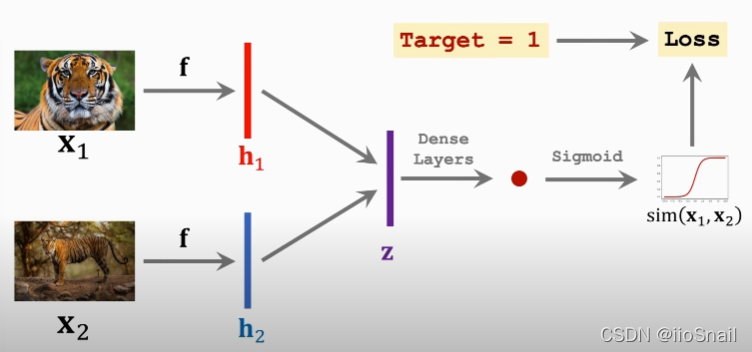
在这里插入图片描述

  • 模型 $f$ ：可以是CNN卷积神经网络；注意：上下两个 $f$ 是同一个网络
  • 向量 $h_1, h_2$：网络 $f$ 的输出向量
  • 向量 $z$：对 $h_1$ 和 $h_2$ 进行处理，例如，令 $z=|h_1-h_2|$
  • Dense Layers：全连接层
  • 在这里插入图片描述：全连接层输出的数值（scalar）

该网络前向传播的过程：

  1. 将两张图片 $x_1$ 和 $x_2$ 分别送给同一个卷积神经网络 $f$ ，得到输出向量 $h_1$ 和 $h_2$
  2. 对 $h_1$ 和 $h_2$ 求差的绝对值，得到向量 $z$
  3. 将向量 $z$ 送给全连接网络，得到一个scalar
  4. 将scalar送给Sigmoid的到最终的输出，最终的输出就是这两张图片的相似度。

对于负样本（Negative Sample）同理。

进阶架构：Triplet Loss
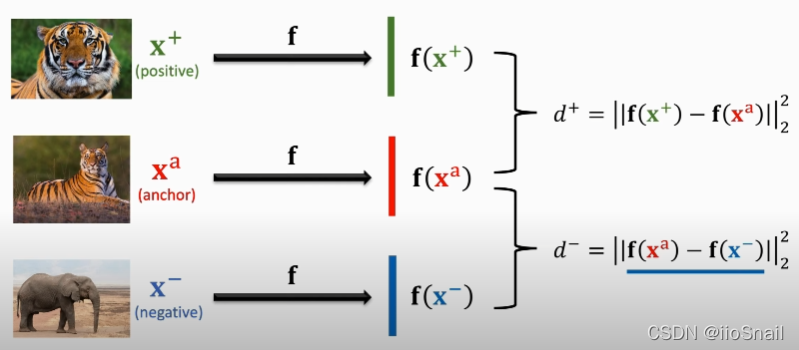
在这里插入图片描述

  1. 从训练集中选取一个样本作为锚点（anchor） $x^a$，然后根据锚点，选择一个正样本 $x^+$ 和一个负样本 $x^-$。
  2. 然后将三个样本送到“同一个”卷积神经网络 $f$ 中，并计算正样本与锚点之间的距离 $d^+$ 和 负样本与锚点之间的距离 $d^-$ 。其中 $d^{+}=\left\|\mathbf{f}\left(\mathbf{x}^{+}\right)-\mathbf{f}\left(\mathbf{x}^{\mathrm{a}}\right)\right\|_{2}^{2}$ ， $d^{-}=|| \mathbf{f}\left(\mathrm{x}^{\mathrm{a}}\right)-\mathbf{f}\left(\mathrm{x}^{-}\right)||_{2}^{2}$。 其中 $|_2^2$ 是二范数的平方。
  3. 显然，我们希望 $d^+$ 越小越好，$d^-$ 越大越好。用图表示则为：

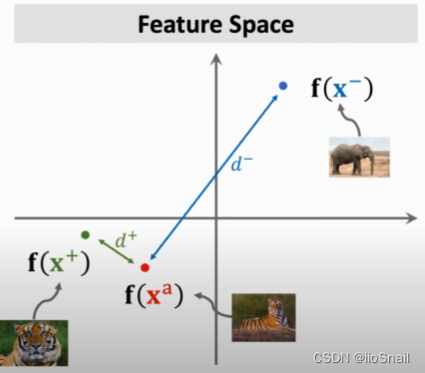
    在这里插入图片描述
  4. 对于损失函数，定义为 $$\begin{aligned}Loss(x^a, x^+, x^-)= max\{0, d^+ +\alpha -d^-\}\end{aligned}$$ 其中 $\alpha$ 为大于0的超参数，含义为：①如果负样本到锚点的距离比正样本到锚点的距离大 $\alpha$，我们就认为分对了，损失函数为0； ②否则，就将 $d^+ + \alpha - d^-$ 作为损失函数

Pretraining and Fine Tuning

另一种熊Few-shot Learning的思路：使用别人预训练好的模型来进行Few-shot Learning。

CNN的预训练模型：用别人训练好的CNN模型，把最后的全连接层砍掉即可。保留下来的卷积层的作用是提取图像的特征，相当于对图像进行了编码（embedding）操作。

具体做法：
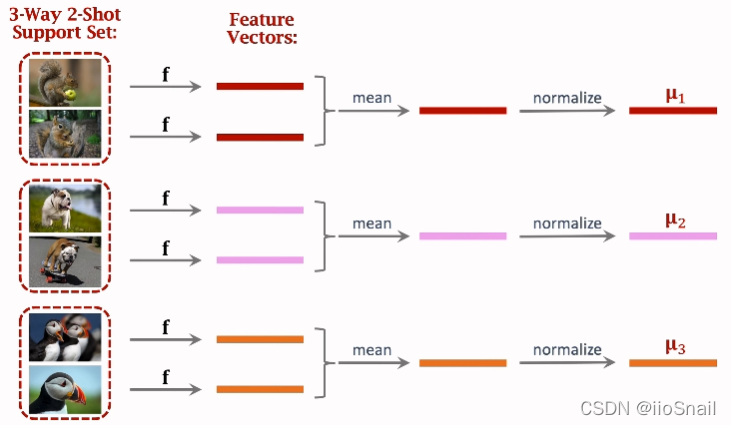
在这里插入图片描述

  1. 用预训练模型 $f$ 对所有的小样本进行特征提取，得到它们的特征向量（feature Vectors）
  2. 将同类别的Feature Vectors进行合并（上图使用的求平均），然后再进行正则化（normalize），最终的得到每个类别的向量 $u_i$
  3. 此时准备工作已经完毕，接下来可以开始做预测了
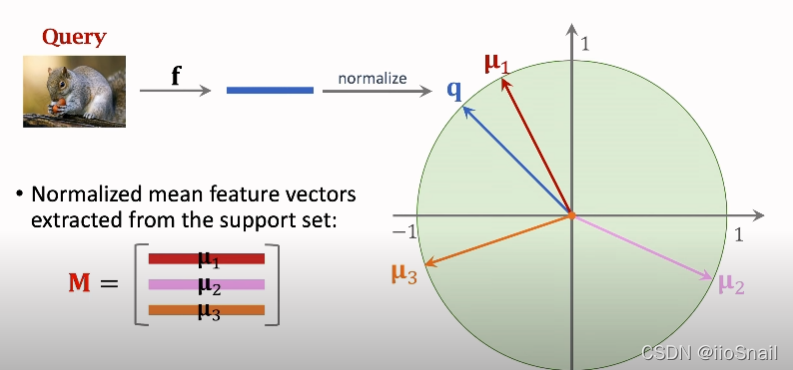
    在这里插入图片描述
  4. 将要预测（query）的图片按照步骤1,2的方式得到向量 $q$
  5. 然后比较向量 $q$ 和类别向量 $u_i$，距离谁最近，那么该图片就是什么类别

计算过程的数学公式为：

$$ \begin{aligned} \textbf{p} = \text{Softmax}(Mq) = \text{Softmax}( \begin{bmatrix} u^T_1q \\ u^T_2q\\ u^T_3q\\ \end{bmatrix}) \end{aligned} $$

选取 $\textbf{p}$ 中数值最大的类别即可。

如何进行Fine Tuning? 上面的方法只用了预训练模型，但并没有对预训练模型进行微调（Fine Tuning），一些文献表示，对预训练模型微调后，效果会更好。

Fine Tuning 思路：把预训练好的CNN的全连接层换成自己的，再用support set 训练一下全连接层就完了。用数学公式表示就是：

$$ \begin{aligned} p_j = \text{Softmax}(W \cdot f(x_j) + b) \end{aligned} $$

其中 $f$ 是不包含全连接层的预训练模型，$W$ 和 $b$ 是自己的全连接层的权重和偏置。损失函数采用 CrossEntropy 即可。

其实，上面没有Fine Tuning的版本就是将 $W$ 固定为 $M$，而 $b$ 固定为0.

Fine Tuning小技巧：

  1. 将 $W$ 初始化为 $M$，$b$ 初始化为0，效果更佳
  2. 损失函数使用Regularization效果会更好
  3. 改造 $Wq$，具体为：将 $wq$ 改为 sim(wq)，听说是可以大幅提高准确率。详见下图：
    在这里插入图片描述

Few-shot常用数据集

  • Omniglot：手写字母识别，适合学术界，只有几M，有1600多个类，但每个类别样本很少
  • Mini-ImageNet：图片识别，有100个类别，每个类别有600个样本


参考资料

参考视频：https://www.youtube.com/watch?v=UkQ2FVpDxHg

Next Post Previous Post
No Comment
Add Comment
comment url