In-Depth Breakdown of Self-Attention, Multi-Head and Masked Attention (Part 2)
Table of Content
1. Introduction
Before reading this article, you should first have a thorough understanding of Self-Attention. I recommend checking out the last article, "In-Depth Breakdown of Self-Attention, Multi-Head and Masked Attention (Part 1)"
2. MultiHead Attention
2.1 Theoretical Explanation of MultiHead Attention
The Transformer uses MultiHead Attention, which is actually very similar to Self-Attention. Let's first clarify a few points before we dive into the explanation:
- No matter how many heads there are in MultiHead Attention, the total number of parameters remains the same. Adding more heads does not increase the number of parameters.
- When MultiHead Attention has only 1 head, it is not equivalent to Self-Attention. MultiHead Attention and Self-Attention are different.
- MultiHead Attention still uses the same formula as Self-Attention.
- In addition to the $W^q, W^k, W^v$ matrices, MultiHead Attention requires an additional $W^o$ matrix.
With these points in mind, we can now begin discussing MultiHead Attention.
The logic of MultiHead Attention is mostly the same as Self-Attention, but it begins to differ after calculating Q, K, and V. So, let's start from here.
Now that we've computed the Q, K, and V matrices, we can directly apply them to the formula for Self-Attention, which is visually represented as:
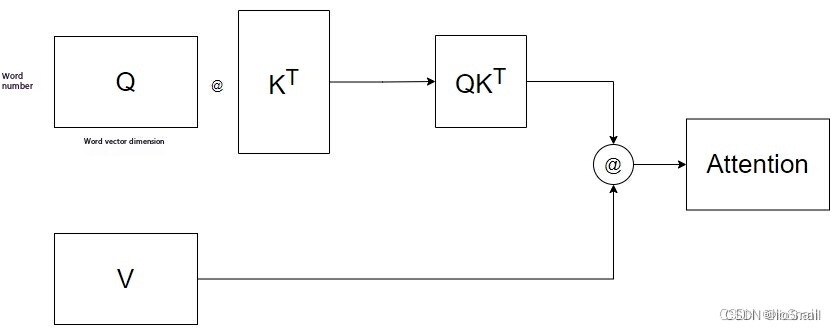
For simplicity, this diagram omits the Softmax and $d_k$ computations.
In MultiHead Attention, before applying the formula, there is one additional step: splitting. The Q, K, and V matrices are split into multiple heads along the "dimension of the word vector," as shown in the following diagram:
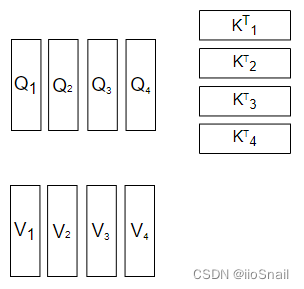
In this example, the number of heads is 4. Once split, the calculations for each head are performed independently, as depicted below:
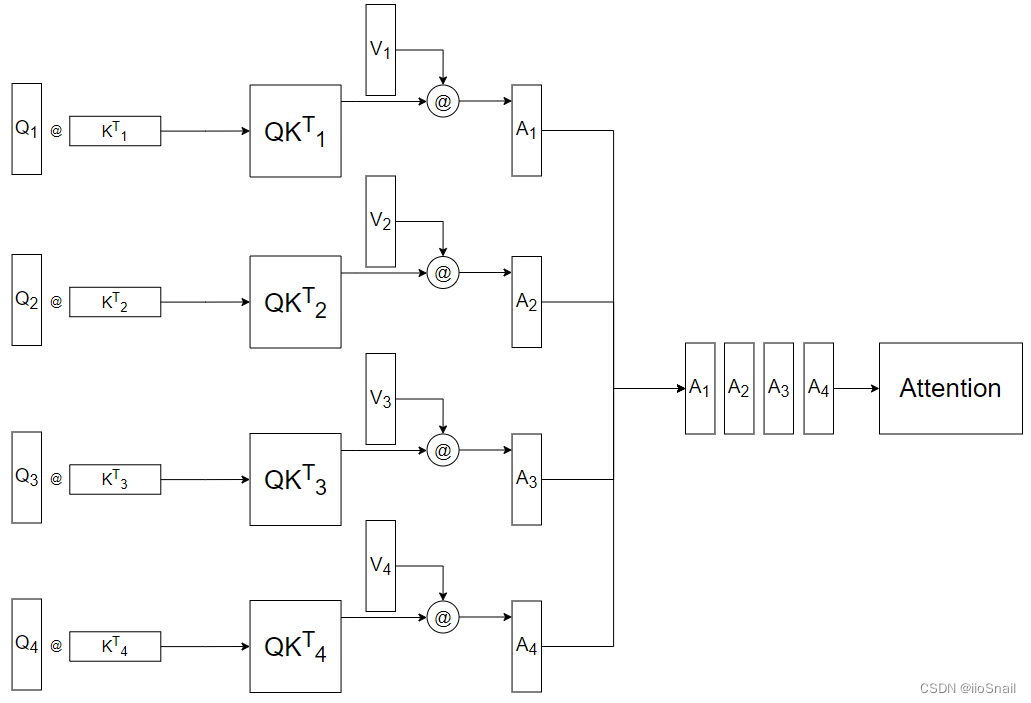
However, directly merging the results of these individual heads using concatenation doesn't yield the best performance, so an additional matrix, $W^o$, is used to apply a linear transformation to the concatenated Attention, as shown here:
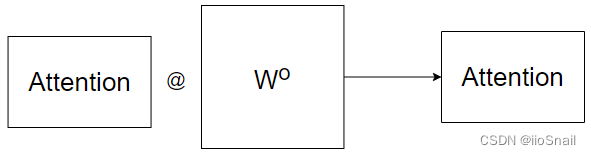
At this point, it's clear that more heads are not always better. So, why use MultiHead Attention at all? The reason given by the Transformer model is that Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. In short, it's better to use more heads than none.。
2.2. Pytorch Implementation of MultiHead Attention
This code is inspired by the project annotated-transformer。
First, we define a general Attention function:
```python
def attention(query, key, value):
"""
Calculate the result of the Attention mechanism.
The inputs here are actually Q, K, and V, and the computation of Q, K, and V is handled within the model.
Please refer to the subsequent MultiHeadedAttention class for more details.
There are two possible shapes for Q, K, and V. If it's Self-Attention, the shape is (batch, sequence_length, d_model),
for example, (1, 7, 128), where batch_size is 1, the sentence has 7 words, and each word has 128 dimensions.
In the case of Multi-Head Attention, the shape is (batch, num_heads, sequence_length, d_model/num_heads),
for example, (1, 8, 7, 16), where batch_size is 1, there are 8 heads, the sentence has 7 words, and 128/8 = 16.
This illustrates that Multi-Head Attention essentially splits the 128 dimensions into 8 heads.
In the Transformer model, since Multi-Head Attention is used, Q, K, and V will always have the second shape.
"""
# Get the value of d_model. This works because query and input share the same shape.
# For Self-Attention, the last dimension is the dimension of word vectors, which is the value of d_model.
# For Multi-Head Attention, the last dimension is d_model / num_heads, where num_heads is the number of heads.
d_k = query.size(-1)
# Compute QK^T / √d_k
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# Apply Softmax to the scores
# p_attn here is a square matrix
# For Self-Attention, the shape will be (batch, sequence_length, sequence_length), for example (1, 7, 7)
# For Multi-Head Attention, the shape will be (batch, num_heads, sequence_length, sequence_length)
p_attn = scores.softmax(dim=-1)
# Finally, multiply by V.
# For Self-Attention, the result will have shape (batch, sequence_length, d_model), which is the final result.
# For Multi-Head Attention, the result will have shape (batch, num_heads, sequence_length, d_model/num_heads).
# This isn't the final output, as the heads need to be merged later, resulting in (batch, sequence_length, d_model).
return torch.matmul(p_attn, value)
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model):
"""
h: Number of attention heads
"""
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume that d_v always equals d_k
self.d_k = d_model // h
self.h = h
# Define the weight matrices W^q, W^k, W^v, and W^o.
self.linears = [
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
]
def forward(self, x):
# Get the batch size
nbatches = x.size(0)
"""
1. Calculate Q, K, V. These are the Multi-Head Q, K, and V, so the shape will be (batch, num_heads, sequence_length, d_model/num_heads)
1.1 First, calculate the Self-Attention Q, K, and V using the defined W^q, W^k, and W^v,
which gives the shape (batch, sequence_length, d_model)
The code for this is: `linear(x)`
1.2 Then split into multiple heads, changing the shape from (batch, sequence_length, d_model) to (batch, sequence_length, num_heads, d_model/num_heads).
The corresponding code is: `view(nbatches, -1, self.h, self.d_k)`
1.3 Finally, swap the "sequence_length" and "num_heads" dimensions, moving the number of heads to the front.
The final shape becomes (batch, num_heads, sequence_length, d_model/num_heads).
The corresponding code is: `transpose(1, 2)`
"""
query, key, value = [
linear(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for linear, x in zip(self.linears, (x, x, x))
]
"""
2. After obtaining Q, K, and V, use the attention function to compute the Attention result.
The shape of x is (batch, num_heads, sequence_length, d_model/num_heads)
The shape of self.attn is (batch, num_heads, sequence_length, sequence_length)
"""
x = attention(
query, key, value
)
"""
3. Merge the multiple heads back together, changing the shape of x from (batch, num_heads, sequence_length, d_model/num_heads)
to (batch, sequence_length, d_model).
3.1 First, swap the "num_heads" and "sequence_length" dimensions, resulting in (batch, sequence_length, num_heads, d_model/num_heads)
The corresponding code is: `x.transpose(1, 2).contiguous()`
3.2 Then merge the "num_heads" and "d_model/num_heads" dimensions, resulting in (batch, sequence_length, d_model)
"""
x = (
x.transpose(1, 2)
.contiguous()
.view(nbatches, -1, self.h * self.d_k)
)
# Finally, apply a linear transformation using the W^o matrix to get the final result.
return self.linears[-1](x)
```
Next, let's try the following:
```python # Define 8 attention heads, with a word vector dimension of 512 model = MultiHeadedAttention(8, 512) # Pass in a batch with size 2, containing 7 words, each with a dimension of 512 x = torch.rand(2, 7, 512) # Output the result after applying Attention print(model(x).size()) ```
The output is:
``` torch.Size([2, 7, 512]) ```
3. Masked Attention
3.1 Why Use a Mask in Attention
In the Transformer’s Decoder, there is a concept called Masked Multi-Head Attention. This section will provide a detailed explanation of this concept.
Let’s start by reviewing the formula for Attention:
$$ \begin{aligned} O_{n\times d_v} = \text { Attention }(Q_{n\times d_k}, K_{n\times d_k}, V_{n\times d_v})&=\operatorname{softmax}\left(\frac{Q_{n\times d_k} K^{T}_{d_k\times n}}{\sqrt{d_k}}\right) V_{n\times d_v} \\\\ & = A'_{n\times n} V_{n\times d_v} \end{aligned} $$
Where:
$$ \begin{aligned} O_{n\times d_v}= \begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix},~~~~A'_{n\times n} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} & \cdots &\alpha'_{n,1} \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots &\alpha'_{n,2} \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix}, ~~~~V_{n\times d_v}= \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix} \end{aligned} $$
Assume that $(v_1, v_2, ... v_n)$ corresponds to the words $(机, 器, 学, 习, 真, 好, 玩)$ Then, $(o_1, o_2, ..., o_n)$ corresponds to $(机', 器', 学', 习', 真', 好', 玩')$. Here, $机'$ contains all the attention information from $v_1$ to $v_n$. The weights for calculating $机'$ come from the first row of $A'$, which is $(\alpha'{1,1}, \alpha'{2,1}, ...)$.
Here, “机器学习真好玩” is a Chinese sentence which means "machine(机器) leaning(学习) is very(真) fun(好玩)"
If you recall the above explanation, let’s now look at how Transformer works. Assume we want to use Transformer to translate the sentence “Machine learning is fun.”
First, we send “Machine learning is fun” to the Encoder, which outputs a tensor called Memory, as shown below:
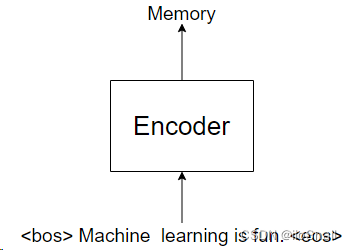
Next, we take the Memory as input to the Decoder for prediction. The Decoder doesn’t produce the entire translation of “Machine learning is fun” all at once, but instead generates one word at a time (or one character at a time, depending on the tokenization method used), as illustrated below:
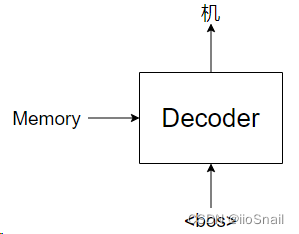
Then, we call the Decoder again, this time with the input <bos> machine:
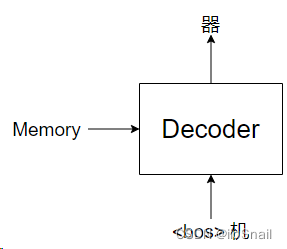
This process continues step by step until the final output is the end token <eos>, signaling the end of the translation:
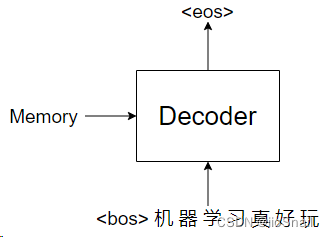
The prediction ends when the Transformer outputs <eos>.
At this point, we can observe that for the Decoder, predictions are made one token at a time. For example, if the input to the Decoder is <bos>机器学, the token "学习" (learning) can only attend to the preceding tokens "机器学" (machine). Thus, for the token "习" (part of the word "学习"), the attention is limited to just those four characters from "机器学习".
However, even when the last input is <bos>machine learning is fun, the token "习" still cannot attend to the later part of the sequence, "真好玩" (is fun). This is where masking comes into play, and the question arises: why do we need this mask? The reason is simple: if the token "习" were allowed to attend to later tokens, its encoding would change.
Let’s break it down:
Initially, we only pass the token "机" (ignoring <bos>), and using the attention mechanism, it might be encoded as $[0.13, 0.73, ...]$.
Next, when we pass the tokens "机器" (machine), the attention mechanism is applied again. If we don’t mask the token "器", the encoding of "机" would change—it would no longer be $[0.13, 0.73, ...]$, but could become something like $[0.95, 0.81, ...]$.
This would cause an issue because the encoding of "机" would no longer be consistent across different steps. In the first step, "机" is encoded as $[0.13, 0.73, ...]$, but in the second step, it might change to $[0.95, 0.81, ...]$. This inconsistency could introduce problems into the network. To prevent this, we use a mask to ensure that the encoding of "机" does not change. Even though "机" might attend to future tokens, it should not actually alter its encoding.
Many articles explain that the purpose of the mask is to prevent the Transformer from leaking information it should not have access to during training. Why is that the case? This is explained in detail in section 3.4.
3.2 How to Apply Masking
To apply masking, all we need to do is modify the scores, which is represented as $A'_{n\times n}$. Let's go through an example:
In the first case, we only have the variable $v_1$, so we have:
$$ \begin{bmatrix} o_1\\ \end{bmatrix}=\begin{bmatrix} \alpha'_{1,1} \end{bmatrix} \cdot \begin{bmatrix} v_1\\ \end{bmatrix} $$
In the second case, we have two variables, $v_1$ and $v_2$:
$$ \begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & \alpha'_{2,1} \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} $$
At this point, if we don't mask $A'_{2\times 2}$, the value of $o_1$ will change (in the first case it is $\alpha'_{1,1}v_1$, but in the second case, it becomes $\alpha'_{1,1}v_1 + \alpha'_{2,1}v_2$). To prevent this, we only need to mask $\alpha'_{2,1}$, ensuring that $o_1$ remains the same across both steps.
So the second case should actually look like this:
$$ \begin{bmatrix} o_1\\ o_2 \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} $$
This process continues, and if we reach the $n$-th step, it would look like this:
$$ \begin{bmatrix} o_1\\ o_2\\ \vdots \\ o_n\\ \end{bmatrix} = \begin{bmatrix} \alpha'_{1,1} & 0 & \cdots & 0 \\ \alpha'_{1,2} & \alpha'_{2,2} & \cdots & 0 \\ \vdots & \vdots & &\vdots \\ \alpha'_{1,n} & \alpha'_{2,n} & \cdots &\alpha'_{n,n} \\ \end{bmatrix} \begin{bmatrix} v_1\\ v_2\\ \vdots \\ v_n\\ \end{bmatrix} $$
3.3 Why Use Negative Infinity Instead of Zero?
According to the above explanation, the mask is zero, but why does the mask in the source code use $-1e9$ (negative infinity)? Here's the relevant part of the Attention code:
```python
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = scores.softmax(dim=-1)
```
If you look closely, the $A'_{n\times n}$ we mentioned earlier is the result after applying softmax. However, in the source code, the masking is done before the softmax operation. This is why the mask is set to negative infinity: after applying softmax to negative infinity, the result becomes zero.
3.4. Masks during Training
When reading articles about Masked Attention online, it's often stated that the purpose of the mask is to prevent the model from seeing content it shouldn't. This section will explain this statement in more detail.
First, let's understand the training process of the Transformer.
During inference, the Transformer generates one word at a time. However, this method is too inefficient for training, so during training, we provide the entire target sequence at once (though you can also follow the inference process). As shown in the diagram below:

From the diagram, we can see the key differences between the Transformer training process and the inference process:
- Source input (src) is the same:For the Transformer inputs (the
srcparameter), they are the same in both training and inference, which is the sentence to be translated. - Target input (tgt) is different:During inference, the target (
tgt) starts with<bos>and then the model adds one word at a time, using the previous output as input for the next step (for example, the second input might be<bos> I). But during training, the entire "complete" target sequence is given to the Transformer at once, which makes it equivalent to providing one word at a time. Here’s another detail: the target sequence (tgt) is one token shorter than the source (src). Ifsrccontains 7 tokens,tgtcontains only 6. This is because during the last inference step, we only provide the firstn-1tokens. For example, if we want to predict<bos> I love you <eos>(ignoring padding), the last input to tgt will be<bos> I love you(without<eos>). Therefore, the input totgtwill never include the last token of the target sequence, which is why we usually remove the last token when processing the target. - Increased number of outputs:During training, the Transformer generates multiple probability distributions at once. For instance, in the diagram above,
我(I) is the output whentgtis<bos>,爱(love) corresponds to when tgt is<bos> 我, and so on. Once we have the output distributions during training, we can calculate the loss without converting the probabilities back into words. One more detail: the number of outputs is 6, corresponding to tokens like我 爱 你 <eos> <pad> <pad>, with the absence of<bos>because it is not predicted. When calculating loss, we compare with these tokens, so the label does not include<bos>. In code, this is often namedtgt_y.
To summarize in one sentence: During Transformer inference, words are predicted one by one, while in training, the entire sequence is fed to the model at once, but the effect is equivalent to predicting one word at a time because of the mask on the target sequence, preventing the model from seeing future words and thus avoiding context information from future words being available to the current ones.
It might still be hard to fully grasp this after reading the summary, so let's run an experiment. The experiment will simulate both the Transformer inference process and the training process, comparing whether providing the entire target sequence during training yields results equivalent to the inference process where words are given one by one.
First, let's define the model:
```python # Vocabulary size is 10, and the word vector dimension is 8 embedding = nn.Embedding(10, 8) # Define the Transformer. Make sure to set it to eval mode, otherwise the output will vary every time. transformer = nn.Transformer(d_model=8, batch_first=True).eval() ```
Next, let's define our src and tgt:
```python # Encoder input src = torch.LongTensor([[0, 1, 2, 3, 4]]) # Decoder input tgt = torch.LongTensor([[4, 3, 2, 1, 0]]) ```
Then, we pass [4] to the Transformer for prediction, simulating the first step in inference:
```python
transformer(embedding(src), embedding(tgt[:, :1]),
# This is used to generate the step-wise mask
tgt_mask=nn.Transformer.generate_square_subsequent_mask(1))
```
```
tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598]]], grad_fn=<NativeLayerNormBackward0>)
```
Now we send [4, 3] to the Transformer, simulating the second step in inference:
```python transformer(embedding(src), embedding(tgt[:, :2]), tgt_mask=nn.Transformer.generate_square_subsequent_mask(2)) ```
```
tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598],
[ 1.2726, -0.3516, 0.6584, 0.3297, 1.1161, -1.4204, -1.5652,
-0.0396]]], grad_fn=<NativeLayerNormBackward0>)
```
At this point, you might notice that the first vector in the output is exactly the same as the one from the previous step.
Finally, we pass the entire tgt to the Transformer, simulating the training process:
```python transformer(embedding(src), embedding(tgt), tgt_mask=nn.Transformer.generate_square_subsequent_mask(5)) ```
```
tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598],
[ 1.2726, -0.3516, 0.6584, 0.3297, 1.1161, -1.4204, -1.5652,
-0.0396],
[ 1.4799, -0.3575, 0.8310, 0.1642, 0.8811, -1.3140, -1.5643,
-0.1204],
[ 1.4359, -0.6524, 0.8377, 0.1742, 1.0521, -1.3222, -1.3799,
-0.1454],
[ 1.3465, -0.3771, 0.9107, 0.1636, 0.8627, -1.5061, -1.4732,
0.0729]]], grad_fn=<NativeLayerNormBackward0>)
```
Notice that the first two tensors are identical to the output from the inference steps. Therefore, by using the mask, we can ensure that the words before won't have information about the words after them. This way, we can ensure that the output of the Transformer won't change depending on how many words are passed in, and we can pass the entire tgt to the Transformer during training without any issues. This is what people often refer to when they talk about preventing the network from seeing things it shouldn't during training.
Try to think about why the output doesn't change. The reason is actually quite simple: the essence of a neural network is the continuous multiplication of matrices, for example: $XW_1W_2W_3\cdots W_n \rightarrow O$, where $X$ is the input and $O$ is the output. In this process, the second row of $X$ will not affect the result of the first row. In the Transformer, the interaction between rows happens due to the Attention mechanism, because it involves operations like $X \cdot X$. However, by using a mask, we ensure that the second row of $X \cdot Mask_X$ does not influence the first row. I won't go into further details here, but you can try calculating it on paper.




