表格汇总

损失函数名称	推荐指数	适用类型	适用模型	Pytorch类	需掌握程度	预测层激活函数
0-1 Loss	✰	二分类	机器学习	无	了解	无
Perceptron Loss	★	二分类	机器学习	无	了解	无
Exponential Loss	★✰	二分类	机器学习	无	了解	无
Hinge Loss	★★	二分类	机器学习	无	了解	无
Ramp Loss	★★✰	二分类	机器学习	无	了解	无
Rescaled Hinge Loss	★★★	二分类	机器学习	无	了解	无
Binary Cross Entropy Loss	★★★★	二分类	机器学习 深度学习	nn.BCELoss	熟练运用	Sigmoid
Cross Entropy Loss	★★★★	多分类	机器学习 深度学习	nn.CrossEntropyLoss	熟练运用	Softmax

本文中损失函数推荐指数、需了解程度等都是我拍脑袋想的，并没有实验或者数据支撑，仅供参考

二分类损失函数

0-1 Loss

推荐指数：★✰✰✰✰

适用范围：二分类

Pytorch类：无

需掌握程度：了解

预测层激活函数：无

公式：

$$ \begin{aligned} L(y, f(x))= \begin{cases}1, \text { if } & y f(x)<0 \\ 0, \text { if } & y f(x) \geq 0\end{cases} ~~~~y \in \{-1,1\} \end{aligned} $$

图像：

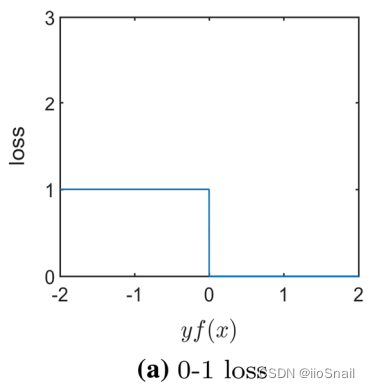
解释：若预测值和真实值符号相同，则loss为0，否则loss为1

Perceptron Loss

推荐指数：★✰✰✰✰

适用范围：二分类

Pytorch类：无

需掌握程度：了解

预测层激活函数：无

公式：

$$ \begin{aligned} L(y, f(x))=\max \{0,-y f(x)\} ~~~~y \in \{-1,1\} \end{aligned} $$

图像：

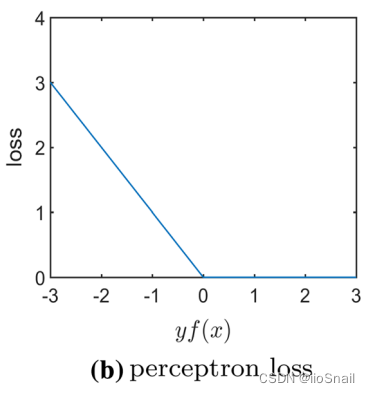
解释：如果预测值与真实值符号相同，则loss为 $0$，否则，loss为 $f(x)$

Exponential Loss

推荐指数：★★✰✰✰

适用范围：二分类

Pytorch类：无

需掌握程度：了解

预测层激活函数：无

提出年份：1995年

公式：

$$ \begin{aligned} L(y, f(x))=e^{-y f(x)} ~~~~其中 ~y \in \{-1,1\} \end{aligned} $$

图像：

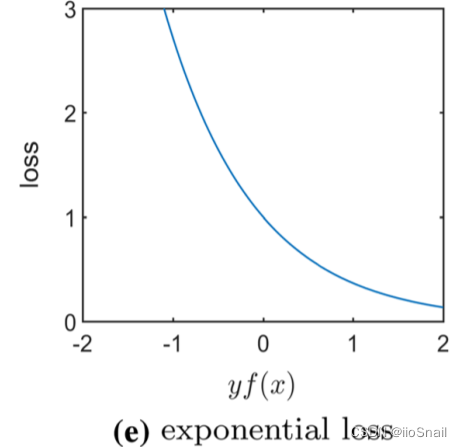
解释：和0-1 Loss类似，如果预测结果$f(x)$与 $y$ 符号一致，则 $|f(x)|$ 越大loss越接近0，反之若$f(x)$与 $y$ 符号不一致，那么$|f(x)|$越大loss越大。

这里的$f(x)$因为没有过sigmoid，所以 $f(x) \in (-\infty, + \infty)$，$f(x)$ 越大，也就越认为Label可能为1，反之同理。

Hinge Loss

推荐指数：★★✰✰✰

适用范围：二分类

Pytorch类：nn.HingeEmbeddingLoss （有区别）

需掌握程度：了解

预测层激活函数：

公式：

$$ \begin{aligned} L(y, f(x)) = \max \{ 0, \text{margin} - yf(x) \}, ~~其中 y\in\{-1,1\},~~\text{margin} 为常数，通常取 1 \end{aligned} $$

图像：

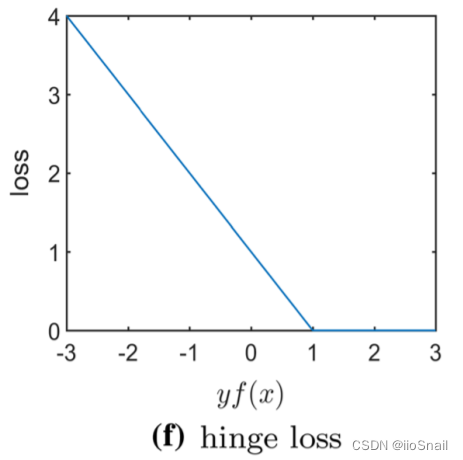
解释：当Label为1时，且预测结果 $f(x) \geq 1$，则loss为0，否则loss就为 $1-f(x)$ 。 当Label为 $-1$ 时，若$f(x) \leq -1$ ，则 loss 为0，否则loss为 $1+f(x)$

上述解释中，我默认 $\text{margin}=1$

Ramp Loss

推荐指数：★★★✰✰

适用范围：二分类

Pytorch类：无

需掌握程度：了解

预测层激活函数：无

公式：

$$ \begin{aligned} L(y, f(x)) = \max \{ 0, 1 - yf(x) \} - \max \{ 0, \text{margin} - yf(x) \}, ~~其中 y\in\{-1,1\},~~\text{margin} 为常数，通常取 -0.5 \end{aligned} $$

图像：

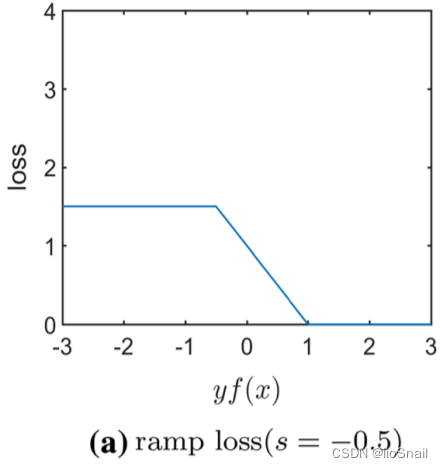
解释：对Hinge Loss进一步优化，当预测Label错误时，也给一个最大的loss。

Rescaled Hinge Loss

推荐指数：★★★✰✰

适用范围：二分类

Pytorch类：无

需掌握程度：了解

预测层激活函数：无

公式：

图像：

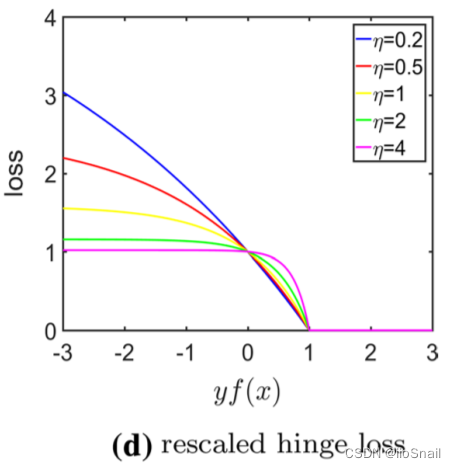
解释：与Ramp Loss类似，在其基础上优化了预测错误的情况，当预测错误时，不设loss上线，而是让其缓慢增长。

Binary Cross Entropy Loss（BCELoss）

推荐指数：★★★★✰

适用范围：二分类

Pytorch类：nn.BCELoss

需掌握程度：熟练运用

预测层激活函数：Sigmoid

公式：

$$ \begin{aligned} L(y, \tilde{p})=-\log \tilde{p} \text {,~~~ where, } \tilde{p}=\left\{\begin{array}{lll} p, & \text { if } & y=1 \\ 1-p, & \text { if } & y = 0 \end{array}\right. ~其中 p \in[0,1] \end{aligned} $$

另一种写法（常见写法）：

$$ \begin{aligned} L(y, p) = y \cdot \log p + (1-y) \cdot \log (1-p) \end{aligned} $$

图像：

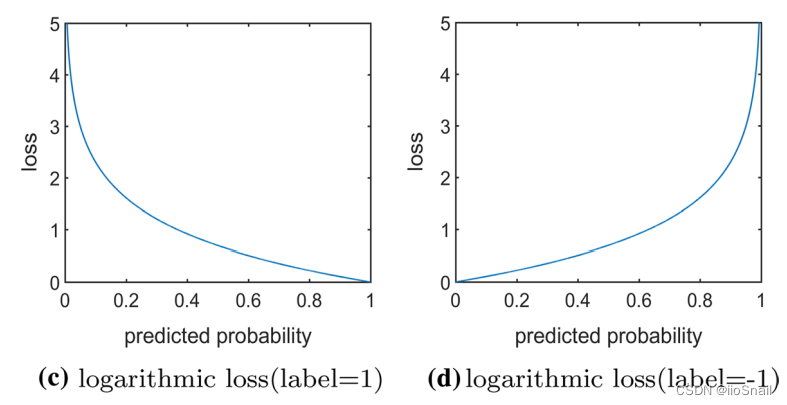
解释：最后的线性层需要通过sigmoid后得到概率 $p$，若标签为 $1$，则损失为 $-\log p$，若标签为 $-1$，则损失为 $-\log (1-p)$

二分类损失函数的发展与比较

我们这里按照逐步迭代的方式来比较这些损失函数，首先，人们提出了 0-1 Loss：

该损失函数缺点明显，其loss取值只有两种，0或1，这样不利于收敛。所以人们提出了Perceptron Loss来解决该问题：

该损失函数函数对预测错误时进行了优化，预测正确时，loss依然为0，但预测错误时，按照错误程度来决定loss大小。但这样还是还是优缺点，当预测正确时，loss完全取0无法展示其有多么正确，例如同样是Label为1，一个预测结果为100，另一个预测结果为0.1 （结果越大说明模型越觉得Label为1），那明显前者预测结果更对。为了体现预测正确时的loss，又引入了 Exponential Loss：

Exponential Loss 对预测正确的情况也增加了损失计算。但同样又引入了新问题，一是对预测错误时的损失惩罚成指数增长，这样数据中中的异常值可能会对模型造成巨大的损害，使模型不够稳定，二是不管预测的有多么对，总是有loss，同样不利于模型的稳定。这两个问题Hinge Loss可以解决：

hinge loss 和perceptron loss很像，但其引入了margin参数。首先，预测错误情况下的loss线性增长缓解了 Exponential Loss中的第一个问题。同时，为预测正确时的结果增加了阈值margin，当预测结果大于margin时，就认为你足够正确了，loss为0，但是如果不够margin，虽然预测正确了，也是会有loss的。 虽然hinge loss缓解了预测错误时损失指数增长的问题，但还是损失还是会无限增长，为了解决该问题，人们又提出了Ramp Loss：

Ramp Loss和hinge loss类似，只不过它对于预测错误的情况给了一个最大loss值，这样就可以避免某些异常数据导致loss过大，进而引起模型不稳定的情况。但如果直接设置loss上限多少有点粗暴，所以人们又提出了另一种方案Rescaled Hinge Loss：

Rescaled Hinge Loss 中，当预测错误时，可以让其loss根据错误程度缓慢增长loss，避免了直接设置最大值。

多分类损失函数

Cross Entropy Loss

推荐指数：★★★★✰

适用范围：多分类

Pytorch类：nn.CrossEntropyLoss

需掌握程度：熟练运用

预测层激活函数：Softmax

公式：

$$ \begin{aligned} L(y, P(y \mid x))=-\log P(y \mid x) \end{aligned} $$

图像：

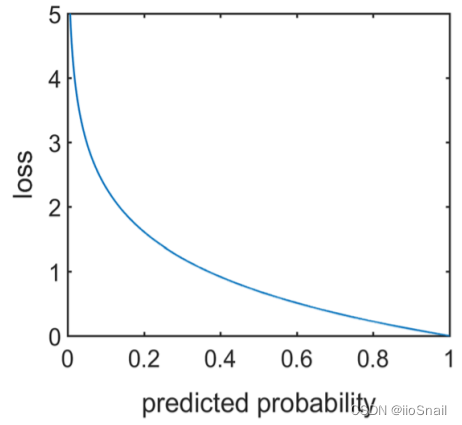
解释：$P(y|x)$ 为预测结果认为是 $y$ 标签的概率，例如类别为 猫、狗、猪，某样本标签为狗，预测结果经过Softmax后得到的概率分布为 $[0.1, 0.7, 0,2]$, 则 $L=-\log 0.7$，底数为 $e$。

---

参考文献

A Comprehensive Survey of Loss Functions in Machine Learning: https://link.springer.com/article/10.1007/s40745-020-00253-5