pytorch 自定义损失函数、优化器(Optimizer)和学习率策略(Scheduler)
文章目录
本节内容
- 梯度下降回顾
- 理解Pytorch模型定义、前向传播、反向传播、更新梯度的过程
- 学会并理解自定义损失函数
- 学会并理解优化器的作用和使用
- 学会并理解自定义学习策略的多种方法
梯度下降回顾
我们首先来简单的回顾一下梯度下降,我们使用一个很简单的例子来说明。
假设我们要进行一元线性回归,即我们想求 $y = \theta x +b$ 中的未知参数 $\theta$ 和 $b$ 。
- 首先我们会对 $\theta$ 和 $b$ 进行初始化,例如,初始化为 $100$ 和 $50$,则我们的初始化方程为:
$$ \begin{aligned} y = \theta x + b = 100 x + 50 \end{aligned} $$
- 之后,我们拿一组样本来带入上述函数,求出这组样本的预测值,这里我们假设只有一组样本 $(x, \hat{y})=(3, 348)$,之后我们会将 $x=3$ 带入到上式中,求出预测值:
$$ \begin{aligned} y = \theta * 3 + b = 100 * 3+ 50 = 350 \end{aligned} $$
- 之后我们使用均方误差损失函数(MSE)来求出损失:
$$ \begin{aligned} L = (y-\hat{y})^2 = (\theta x+b - \hat{y})^2 =(350-348)=2 \end{aligned} $$
- 与此同时,我们可以对使用损失函数 $L$ 对 $\theta$ 和 $b$ 进行求导,来算出他们的梯度:
$$ \begin{aligned} \frac{\partial L}{\partial \theta} = 2(\theta x+b-\hat{y})x=2(100*3+50-348)*3 = 12 \end{aligned} $$
$$ \begin{aligned} \frac{\partial L}{\partial b} = 2(\theta x + b- \hat{y}) = 2(100*3+50-348)=4 \end{aligned} $$
- 然后就可以使用优化器(Optimizer)更新 $\theta$ 和 $b$ 参数了,如果使用SGD,那就是如下公式,假设学习率是2:
$$ \begin{aligned} \theta \leftarrow \theta - lr * \frac{\partial L}{\partial \theta} = 100 - 2*12=76 \end{aligned} $$
$$ \begin{aligned} b \leftarrow \theta - lr * \frac{\partial L}{\partial b} = 50 -2*4=42 \end{aligned} $$
- 最终,在一次迭代后,$\theta$ 变为了 $76$, $b$ 变为了$42$,即:
$$ \begin{aligned} y = \theta x + b = 76 x+42 \end{aligned} $$
Pytorch 实现梯度下降与参数更新
本节我们来对上一节的例子使用Pytorch进行实验,来感受一下Pytorch的梯度下降:
- 首先我们会对 $\theta$ 和 $b$ 进行初始化,例如,初始化为 $100$ 和 $50$,我们的初始化代码为:
```python theta = Variable(torch.FloatTensor([100]), requires_grad=True) # θ b = Variable(torch.FloatTensor([50]), requires_grad=True) x = 3 y_hat = 348 # 真实值 ```
由于 theta 和 b 是需要求梯度的,所以用Variable封装
- 接下来我们将 $x$ 带入到 $y = \theta x + b$ 中求出预测值:
```python y = theta * x + b y ```
输出为:
``` tensor([350.], grad_fn=<AddBackward0>) ```
- 之后我们使用均方误差损失函数(MSE)来求出损失:
```python L = (y-y_hat) ** 2 L ```
输出为:
``` tensor([4.], grad_fn=<PowBackward0>) ```
- 接下来,我们使用损失对需要L函数中的变量进行求导:
```python
L.backward()
print("theta.grad:", theta.grad)
print("b.grad:", b.grad)
```
输出为:
``` theta.grad: tensor([12.]) b.grad: tensor([4.]) ```
- 然后就可以使用优化器更新 $\theta$ 和 $b$ 参数了,这里使用SGD,学习率为2:
```python
optimizer = torch.optim.SGD([theta, b], lr=2) # 传入要更新的参数和学习率
optimizer.step() # 更新参数
print("theta:", theta)
print("b:", b)
```
- 最终,在一次迭代后,$\theta$ 变为了 $76$, $b$ 变为了$42$
在看完这个例子后,相信你已经知道pytorch的模型、损失函数、优化器在整个模型训练中都扮演者什么样的作用了,其实就是以下几点:
- 模型的作用其实就是执行一系列的函数运算,在上述例子中模型就是
y = theta * x + b,入参为 $x$,调用forward也就是执行该式子 - 损失函数其实也是执行一系列函数运算,在上述例子就是
L = (y-y_hat) ** 2,所以其实损失函数和模型在Pytorch中并没有什么本质的区别,它们都是继承nn.Module。只是模型A(模型)的输出作为模型B(损失函数)的输入又进行了一些计算,只不过最后计算梯度的时候是对模型B进行求微分,也就是上面的L.backward() - 最后,要将变量的梯度更新到变量上,这时候就是优化器出场了,它负责执行公式$\theta \leftarrow \theta - lr * \frac{\partial L}{\partial \theta}$。因为在更新梯度上,并不是简单的梯度乘以学习率,不同的人有不同的想法,所以才会出现Adam等不同的优化器。
自定义损失函数
看完了上面两节,自定义损失函数应该就不攻自破了。其实损失函数就是定义一个模型,再多进行一步前向传递即可。这里我们将上一节的例子再进行一下改造。
首先,我们定义出我们的模型:
```python
class SimpleModel(nn.Module):
def __init__(self):
super(SimpleModel, self).__init__()
# 补充:这里正确的做法应该是使用nn.Parameter进行封装。
# nn.Parameter的作用是将该参数作为模型参数。
# 这样才能在调用model.parameters()时获取到。
self.theta = Variable(torch.FloatTensor([100]), requires_grad=True) # θ
self.b = Variable(torch.FloatTensor([50]), requires_grad=True)
def forward(self, x):
return self.theta * x + self.b
```
接下来定义损失函数:
```python
class SimpleMSELoss(nn.Module):
def __init__(self):
super(SimpleMSELoss, self).__init__()
def forward(self, y, y_hat):
return (y - y_hat) ** 2
```
读者们可以尝试下如何把它们两个合并
最后我们来使用一下:
```python
x = 3
y_hat = 348 # 真实值
model = SimpleModel()
criteria = SimpleMSELoss()
y = model(3)
loss = criteria(y, y_hat)
loss.backward()
print("theta.grad:", model.theta.grad)
print("b.grad:", model.b.grad)
```
输出为:
``` theta.grad: tensor([12.]) theta.b: tensor([4.]) ```
自定义优化器
在Pytorch中自定义优化器需要继承基类torch.optim.Optimizer,然后实现其step方法即可。
Optimizer的部分源码如下:
```python
class Optimizer(object):
def __init__(self, params, defaults):
...
param_groups = list(params)
...
if not isinstance(param_groups[0], dict):
param_groups = [{'params': param_groups}]
...
def step(self, closure):
raise NotImplementedError
```
Optimizer的初始化方法需要两个必填参数:
- params:这个就是模型参数,严格来说应该是要进行更新的参数。Optimizer会将其放在param_groups这个变量下
- defaults:这个是模型的一些默认配置。传空字典也没关系
Optimizer最重要的是step方法,这个是用户需要进行参数更新的地方,用户需要自己实现该方法,通常是从param_groups拿出模型参数,然后进行更新。
我们还接着之前的例子,实现一个简单的优化器,我们优化器的需求是:和SGD类似,但是每次学习率都乘以一个[0-1]的随机数。代码如下:
```python
class MyOptimizer(Optimizer):
def __init__(self, params, lr):
self.lr = lr
super(MyOptimizer, self).__init__(params, {})
def step(self, closure=False): # 这个closure我也不知道干啥的,应该不重要
random_num = 0.4 # 假设生成的随机数为0.4
for param_group in self.param_groups:
params = param_group['params']
# 从param_group中拿出参数
for param in params:
# 循环更新每一个参数的值
param.data = param.data - self.lr * random_num * param.grad
```
然后用法和内置的Optimizer一致:
```python
optimizer = MyOptimizer([model.theta, model.b], lr=2)
optimizer.step()
print("theta:", model.theta)
print("b:", model.b)
```
输出为:
``` theta: tensor([90.4000], requires_grad=True) b: tensor([46.8000], requires_grad=True) ```
自定义学习率策略
要定义学习策略,其实最好的方式就是把他集成在Optimizer中,例如torch.optim.Adagrad就是这么做的。但很多时候我们并不想改变原有的复杂算法,只是想对他的学习率动一下手脚,此时就用到了自定义学习策略。
Pytorch实现了很多自定义学习策略,具体可参考该链接。
我们先使用一个Pytorch实现好的,来看一下怎么用。假设需求为:更新100次参数,每10步将学习率减小一半。针对这个需求,我们可以使用torch.optim.lr_scheduler.StepLR来完成。代码如下:
```python
epoch = 100 # 循环100次,每一个epoch更新一次参数
theta_list = [] # 记录一下theta的变化
# 1.初始化要更新的参数theta,初始化为1
theta = Variable(torch.FloatTensor([1]), requires_grad=True)
# 2. 定义SGD优化器,学习率设为0.1
optimizer = torch.optim.SGD([theta], lr=0.1)
# 3. 定义学习率策略,每{step_size}步,学习率乘以{gamma}
lr_scheduler = StepLR(optimizer, step_size=10, gamma=0.5)
# 4. 开始进行模型训练
for i in range(epoch):
# 4.1 手动设置theta的梯度为0.1
theta.grad = torch.FloatTensor([0.1])
# 4.2 将梯度更新到theta参数上
optimizer.step()
# 4.3 调整学习率。注意:调整学习率要放在`optimizer.step()`之后
lr_scheduler.step()
# 4.4 清空梯度
optimizer.zero_grad()
# 记录一下theta的变化
theta_list.append(theta.item())
# 打印一下学习率和theta参数
print("epoch:{}, lr:{}, theta:{}".format(i, optimizer.param_groups[0]['lr'], theta.item()))
# 5.绘制theta变化
plt.plot(range(epoch), theta_list)
plt.show()
```
输出为:
``` epoch:0, lr:0.1, theta:0.9900000095367432 epoch:1, lr:0.1, theta:0.9800000190734863 ... 略 epoch:8, lr:0.1, theta:0.9100000858306885 epoch:9, lr:0.05, theta:0.9000000953674316 epoch:10, lr:0.05, theta:0.8950001001358032 ...略 epoch:18, lr:0.05, theta:0.8550001382827759 epoch:19, lr:0.025, theta:0.8500001430511475 epoch:20, lr:0.025, theta:0.8475001454353333 ... 略 ```
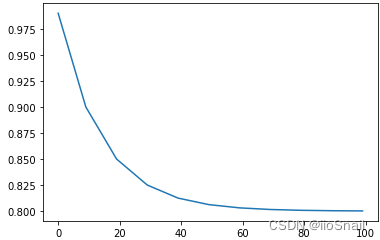
上述例子中,我使用了0.1学习率的来对参数theta进行更新,而参数theta的梯度每次都固定为1。可以看到,前9次theta每次都是下降0.01。从第10次开始,学习率减小了一半,然后每隔10次学习率都会减小一半。
使用 LambdaLR 实现简单的学习率策略
通常我们的学习率策略并不是很复杂,此时我们可以使用Pytorch提供的torch.optim.lr_scheduler.LambdaLR 来实现,该方法接收两个重要参数:
optimizer:该参数就是优化器对象,每个学习率策略都要传lr_lambda:该参数接收一个函数,该函数有一个参数last_epoch,表示上次是第几个epoch(其实指的就是你之前调用过几次lr_scheduler.step())。你可以通过该参数自定义你的学习率策略,优化器在实际执行时使用的学习率会乘以该函数的返回结果,即lr * lr_lambda(last_epoch)。注意,这里的lr是你定义Optimizer时传入的那个学习率,而且始终不变。
例如,要实现前面的每10次将学习率降低一半,我们可以这么写:
```python lr_scheduler = LambdaLR(optimizer, lr_lambda=lambda epoch: 0.5 ** (epoch // 10)) ```
通过继承 _LRScheduler 实现自定义的学习率策略
可能你的学习率策略比较复杂,LambdaLR 也无法满足你,此时你就要自己实现一个学习率策略。
Pytorch中,所有的学习率策略都要继承基类 torch.optim.lr_scheduler._LRScheduler,并实现该基类的一个重要方法def get_lr(self),你只需要按照你的学习率策略返回学习率即可。
但要实现你的学习率策略,你可能还需要用到_LRScheduler类的这些方法和属性:
self.last_epoch:获取之前执行了多少次lr_scheduler.step()了self.base_lrs:基础学习率,也就是定义Optimizer时指定的那个学习率。注意,这个是一个list,可能是因为Optimizer要更新的那些参数也不一定就是使用同一个学习率,一般只有一个。同理,get_lr方法也要返回一个list,且数量与self.base_lrs相同。self.optimizer:你可以通过该属性得到优化器对象。你可以通过代码[group['lr'] for group in self.optimizer.param_groups]获取到优化器中的学习率。你的学习率策略改变的就是这个值。self.get_last_lr():获取上次的学习率。这个方法其实就是返回了属性self._last_lr。但这里有个坑,self._last_lr是在第一次调用step()方法后才会生成,所以使用的时候可能会报错,你可以通过在__init__方法中初始化self._last_lr来避免报错。
有了上述这些方法,我们就可以自定义学习率策略来实现前面的每10次将学习率降低一半的策略了,代码如下:
```python
class MyLR(_LRScheduler):
def __init__(self, optimizer):
# 初始化self._last_lr避免报错
self._last_lr = [group['lr'] for group in optimizer.param_groups]
# 在_LRScheduler的初始化时,会调用step()方法
super(MyLR, self).__init__(optimizer)
def get_lr(self):
# 获取之前的学习率
last_lrs = self.get_last_lr()
if self.last_epoch != 0 and self.last_epoch % 10 == 0:
# 每10个epoch将学习率降低一半
return [lr * 0.5 for lr in last_lrs]
else:
return last_lrs
lr_scheduler = MyLR(optimizer)
```
通过手动更新Optimizer中的学习率来自定义学习策略
其实要自定义学习策略不一定非要向上述说的那样那么麻烦,你可以直接像如下代码直接更新optimizer中的学习率:
```python
for p in optimizer.param_groups:
p['lr'] = rate
```
这样其实就灵活多了,我可以自定义一个普通类来记录学习率策略需要用到的东西,然后使用上述代码更新即可。例如:
```python
epoch = 100 # 循环100次,每一个epoch更新一次参数
theta_list = [] # 记录一下theta的变化
# 1.初始化要更新的参数theta,初始化为1
theta = Variable(torch.FloatTensor([1]), requires_grad=True)
# 2. 定义SGD优化器,学习率设为0.1
optimizer = torch.optim.SGD([theta], lr=0.1)
# 3. 开始进行模型训练
for i in range(epoch):
# 3.1 手动设置theta的梯度为0.1
theta.grad = torch.FloatTensor([0.1])
# 3.2 将梯度更新到theta参数上
optimizer.step()
"""
直接调整optimizer的学习率
"""
for p in optimizer.param_groups:
if (i + 1) % 10 == 0:
p['lr'] = p['lr'] * 0.5
# 3.4 清空梯度
optimizer.zero_grad()
# 记录一下theta的变化
theta_list.append(theta.item())
# 打印一下学习率和theta参数
print("epoch:{}, lr:{}, theta:{}".format(i, optimizer.param_groups[0]['lr'], theta.item()))
# 4.绘制theta变化
plt.plot(range(epoch), theta_list)
plt.show()
```
参考资料
torch.optim.lr_scheduler._LRScheduler Class Reference:https://www.ccoderun.ca/programming/doxygen/pytorch/classtorch_1_1optim_1_1lr__scheduler_1_1__LRScheduler.html
SOURCE CODE FOR TORCH.OPTIM.LR_SCHEDULER
torch.optim.lr_scheduler:调整学习率: https://blog.csdn.net/qyhaill/article/details/103043637



