中文 | English

Introduction to Einsum

You might have heard about einsum somewhere, but couldn't figure out how to use it or understand it. This article will guide you step by step on how to use it (this is a general approach—once you learn the method, you'll understand it fully).

What is the Einsum Function?

"Ein" comes from Einstein, and "sum" stands for summation. einsum refers to the Einstein summation convention, which essentially eliminates the summation signs. It's that simple. Here's an example:

We have a matrix:

$$ \begin{aligned} A_{2\times 2} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \end{aligned} $$

We want to sum over the "rows" of matrix A to get a new matrix B (or vector B). The formula for this would be:

$$ \begin{aligned} B_{i} = \sum_j A_{ij} = B_2 = \begin{pmatrix} 3 \\ 7 \end{pmatrix} \end{aligned} $$

As for the summation sign, Einstein thought it looked a bit redundant and decided to omit it. So, the formula simplifies to:

$$ \begin{aligned} B_i = A_{ij} \end{aligned} $$

If we express this with einsum, it would be: torch.einsum("ij->i", A). The -> symbol acts like an equal sign, where the ij on the left of -> corresponds to $A_{ij}$, and the i on the right corresponds to $B_i$. The first argument passed to einsum is the einsum expression, and the following arguments represent the matrices on the right side of the equation.

Here, the indices $i$ and $j$ refer to the subscripts of A, but you can use different letters if you prefer.

Note: einsum is not exclusive to PyTorch. You can find it in other libraries like NumPy and TensorFlow as well.

By now, if you're quick on the uptake, you may have already grasped the concept. But for those still confused, like I was at first, I'll explain how to interpret an einsum expression and how to write one yourself.

How to Understand an Einsum Expression

When we encounter an einsum expression, the first step is to write its corresponding mathematical expression. For example, let's consider the following einsum expression:

```python
A = torch.Tensor(range(2*3*4)).view(2, 3, 4)
C = torch.einsum("ijk->jk", A)
```

The corresponding mathematical expression for this is:

$$ \begin{aligned} C_{jk} = A_{ijk} \end{aligned} $$

The second step is to add the summation symbol $\sum$. How do we do this, and where do we place it? This depends on the difference between the subscripts on both sides. The summation symbol corresponds to the difference between the right-hand side and the left-hand side indices. In this example, the right-hand side has $ijk$, while the left-hand side is $jk$, which means there is a difference of one $i$. Hence, we add $\sum_i$. The final equation becomes:

$$ \begin{aligned} C_{jk} = \sum_i A_{ijk} \end{aligned} $$

The third step is to visualize or mentally simulate what this equation does. This can be depicted as:

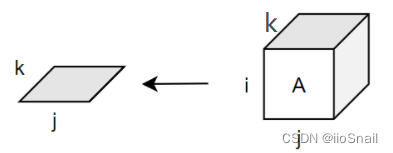
From this diagram, it's easy to see that it's summing over the $i$ dimension, which is equivalent to C = A.sum(dim=0).

The fourth step is to attempt reproduce the operation with a for loop. Einsum is actually quite easy to reproduce; just follow the formula and write out the for loop. Use += for summation.

```python
i, j, k = A.shape[0], A.shape[1], A.shape[2] # Get the dimensions i, j, k
C_ = torch.zeros(j, k) # Initialize C_ to store the result
for i_ in range(i): # Iterate over i
    for k_ in range(k): # Iterate over j
        for j_ in range(j): # Iterate over k
            C_[j_][k_] += A[i_][j_][k_] # Summation
```

```python
C, C_
```

```
(tensor([[12., 14., 16., 18.],
         [20., 22., 24., 26.],
         [28., 30., 32., 34.]]),
 tensor([[12., 14., 16., 18.],
         [20., 22., 24., 26.],
         [28., 30., 32., 34.]]))
```

As we can see, the result from our for loop matches the result from einsum.

That’s it! Now you know how to understand einsum. Just follow the four steps outlined above and practice often.

How to Understand an Einsum Expression (Practice)

Let’s practice a few examples. We'll start with a simple one.

```python
A = torch.Tensor(range(2*3)).view(2, 3)
B = torch.einsum("ij->ji", A)
```

Step 1: Write the mathematical expression:

$$ \begin{aligned} B_{ji} = A_{ij} \end{aligned} $$

Step 2: Add the summation symbol. Here, the indices on the left are $ji$, and on the right are $ij$. The number of indices matches perfectly, so there's no need (and should not) to add the summation symbol.

Step 3: Visualize the matrix transformation process:

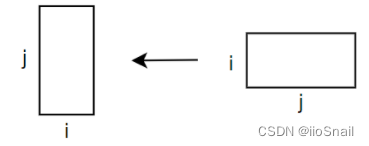
Oh, this is simply the transpose of the matrix.

Step 4: Implement the process using a for loop:

```python
i, j = A.shape[0], A.shape[1] # Get i, j
B_ = torch.zeros(j, i) # Initialize B_ to store the result
for i_ in range(i): # Iterate over i
    for j_ in range(j): # Iterate over j
        B_[j_][i_] = A[i_][j_]  # No summation here, so use = instead of +=
```

```python
B, B_
```

```
(tensor([[0., 3.],
         [1., 4.],
         [2., 5.]]),
 tensor([[0., 3.],
         [1., 4.],
         [2., 5.]]))
```

---

Now, let's move on to a more complicated example.

```python
A = torch.Tensor(range(2*3*4*5)).view(2, 3, 4, 5)
B = torch.Tensor(range(2*3*7*8)).view(2, 3, 7, 8)
C = torch.einsum("ijkl,ijmn->klmn", A, B)
```

When there are multiple matrices on the right-hand side, they are separated by commas.

Step 1: Write the mathematical expression:：

$$ \begin{aligned} C_{klmn} = A_{ijkl}B_{ijmn} \end{aligned} $$

Step 2: Add the summation symbols. On the right side, we have the indices $ijklmn$, while on the left, we only have $klmn$. The left side is missing $ij$, so we need to add two summation signs, $\sum_i \sum_j$. The final expression is:

$$ \begin{aligned} C_{klmn} =\sum_i \sum_j A_{ijkl}B_{ijmn} \end{aligned} $$

Note that $A_{ijkl}$ and $B_{ijmn}$ are not being multiplied as matrices; instead, they are multiplied element-wise because both $A_{ijkl}$ and $B_{ijmn}$ are individual numbers.

Step 3: Visualize the matrix transformation process. It’s too complex to illustrate in 4D, so you’ll have to imagine it.

Step 4: Implement the process using a for loop.

```python
i,j,k,l,m,n = A.shape[0],A.shape[1],A.shape[2],A.shape[3],B.shape[2],B.shape[3]
C_ = torch.zeros(k,l,m,n)
for i_ in range(i):
    for j_ in range(j):
        for k_ in range(k):
            for l_ in range(l):
                for m_ in range(m):
                    for n_ in range(n):
                        C_[k_][l_][m_][n_] += A[i_][j_][k_][l_]*B[i_][j_][m_][n_]
```

```python
C == C_
```

```
tensor([[[[True, True, True,  ..., True, True, True],
          ...........................
          [True, True, True,  ..., True, True, True]]]])
```

The Special Usage of einsum

(1) If the left-hand side of the equation is just a number, then nothing needs to be written on the left side of ->. For example:

$$ \begin{aligned} b = \sum_{ijk} A_{ijk} \end{aligned} $$

```python
A = torch.Tensor(range(1*2*3)).view(1, 2, 3)
b = torch.einsum("ijk->", A) # 由于b是一个数，没有下标，所以->右边什么都不用写
b
```

```
tensor(15.)
```

---

(2) If there are too many subscripts or it's uncertain, they can be omitted. For example:

$$ \begin{aligned} B_{*} = \sum_{i} A_{i*} \end{aligned} $$

```python
A = torch.Tensor(range(1*2*3)).view(1, 2, 3)
B = torch.einsum("i...->...", A)  # Ellipsis refers to *
B.size()
```

```
torch.Size([2, 3])
```

By now, you should be able to understand einsum expressions. If you still don't understand, it's probably due to the complexity of the formula itself. Some summation formulas are indeed complicated, so you can break them down step by step and see what they represent.

How to Write an einsum Expression

Writing an einsum expression is also simple. Just reverse the steps mentioned above:

1. First draw the matrix operations you need to perform;
2. Try to implement it with a for-loop;
3. Write the mathematical expression;
4. Write the einsum expression and validate it.

Next, let's demonstrate with the matrix multiplication formula.

Step 1: Draw the matrix multiplication process, as shown below:

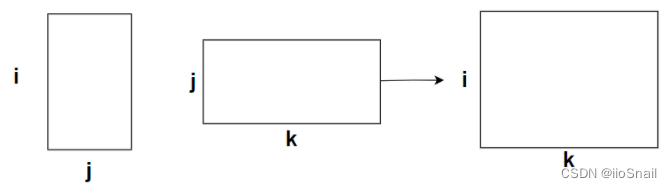
Step 2: Try implementing it with a for-loop:

```python
A = torch.Tensor(range(2*3)).view(2, 3)
B = torch.Tensor(range(3*4)).view(3, 4)
C = torch.zeros(i, k)
i, j, k = 2, 3, 4
for i_ in range(i):
    for j_ in range(j):
        for k_ in range(k):
            C[i_][k_] += A[i_][j_]*B[j_][k_]
```

Step 3: Write the mathematical expression:

$$ \begin{aligned} C_{ik} = A_{ij}B_{jk} \end{aligned} $$

Step 3.2: Add the summation symbol. The left side has indices $ik$, the right side has $ijk$, but $j$ is missing, so we add $\sum_j$:

$$ \begin{aligned} C_{ik} = \sum_j A_{ij}B_{jk} \end{aligned} $$

Step 4: Write the einsum expression and validate it:

```python
D = torch.einsum("ij,jk->ik", A, B) 
E = A@B
```

```python
C, D, E
```

```
(tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]),
 tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]),
 tensor([[20., 23., 26., 29.],
         [56., 68., 80., 92.]]))
```

---

References

• einsum is all you need: https://www.youtube.com/watch?v=pkVwUVEHmfI