直观的感受一下范数

先直观的感受一下二维空间的范数，假设在二维空间的向量为 $\mathbf{v} =(x,y)$

则v的1范数为：

$$ \begin{aligned} ||\mathbf{v}||_1 =||(x,y)||_1 = |x| + |y| = (|x|^1+|y|^1)^\frac{1}{1} \end{aligned} $$

v的2范数为：

$$ \begin{aligned} ||\mathbf{v}||_2 =||(x,y)||_2 = \sqrt{|x|^2 + |y|^2} = (|x|^2+|y|^2)^\frac{1}{2} \end{aligned} $$

v的3范数为：

$$ \begin{aligned} ||\mathbf{v}||_3 =||(x,y)||_3 = \sqrt[3]{|x|^3 + |y|^3} = (|x|^3+|y|^3)^\frac{1}{3} \end{aligned} $$

推广后，得v的p范数为：

$$ \begin{aligned} ||\mathbf{v}||_p =||(x,y)||_p = \sqrt[p]{|x|^p + |y|^p} = (|x|^p+|y|^p)^\frac{1}{p} \end{aligned} $$

当 $p=\infty$ 时，有些区别，v的无穷范数为：

$$ \begin{aligned} ||\mathbf{v}||_\infty =||(x,y)||_\infty = max(|x|, |y|) \end{aligned} $$

为无穷范数时，是从x,y的绝对值中挑出一个大的

范数的定义

感受过二维向量的范数后，将其扩展到n维向量后，向量$x$的范数为：

向量$x$的1范数：

$$ \begin{aligned} ||x||_1 = \sum_{i=1}^n|x_i| \end{aligned} $$

向量$x$的2范数： $$ \begin{aligned} ||x||_2 = (\sum_{i=1}^n|x_i|^2)^\frac{1}{2} \end{aligned} $$

向量$x$的p范数： $$ \begin{aligned} ||x||_p = (\sum_{i=1}^n|x_i|^p)^\frac{1}{p} ~~~~ 1 \le p < \infty \end{aligned} $$

注意p的范围：①p不能等于无穷，对于无穷范数有额外的定义；②p可以是小数

向量$x$的无穷范数：

$$ \begin{aligned} \|x\|_{\infty}=\max _{1 \leq i \leq n}\left|x_{i}\right| \end{aligned} $$

直观的感受下范数的边界图像

定义范数后，可以直观的感受下二维范数的边界图像，即 $\|(x,y)\|_p\le1$ 的函数图像。

1范数时的边界图像（$|x|+|y|=1$ 的图像）为：

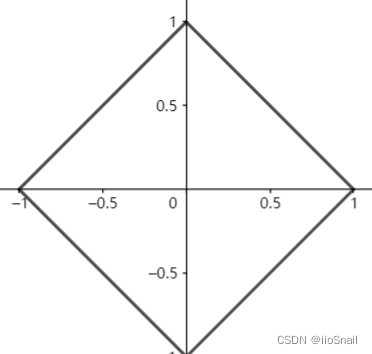
菱形边界是函数 $|x|+|y|=1$ 函数图像，菱形内部满足 $|x|+|y| < 1$。其他范数同理

2范数时的边界图像（$\sqrt{|x|^2+|y|^2}=1$ 的图像）为：

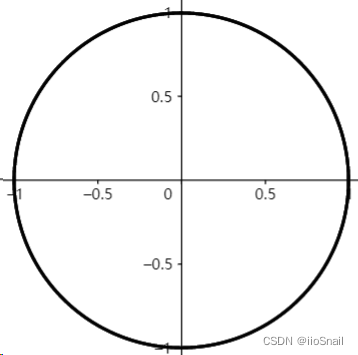
可以通过GeoGebra p-norm ball，自己感受下不同范数下的边界图像

通过感受不同范数的图像最终可以发现如下图所示的规律，即范数越大，图像越方。同时容易明白，为什么二维无穷范数的定义是 $max(|x|, |y|)$

对于三维空间，那就是遵循下图的变化：

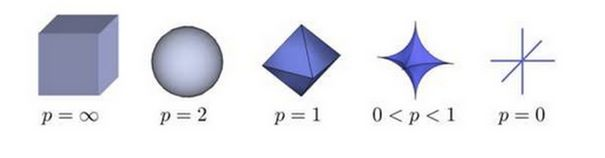
范数的性质

1. 正定型： $\|x\| \ge0$ ，当且仅当 $x=0$时，$\|x\|=0$
2. 齐次性：$\|\lambda x\|=|\lambda|\|x\|$, 其中 $\lambda \in R$
3. 三角不等式：$\|x+y\| \leq\|x\|+\|y\|, \forall x, y \in C^{n}$
4. $\|0\|=0$
5. 当 $x\neq0$ 时，$\|\frac{1}{\|x\|}x \|=1$
6. 对任意的 $x\in C^n$，有 $\|-x\|=\|x\|$
7. 对任意的 $x, y\in C^n$，有 $|~\|x\|-\|y\|~| \le \|x-y\|$

---

参考资料

GeoGebra p-norm ball：https://www.geogebra.org/m/pyxfvyyk

第八课：向量的范数：https://zhuanlan.zhihu.com/p/30279795