1. 什么是线性回归

假设我们现在要预测房价，我们现在采样了一些数据：

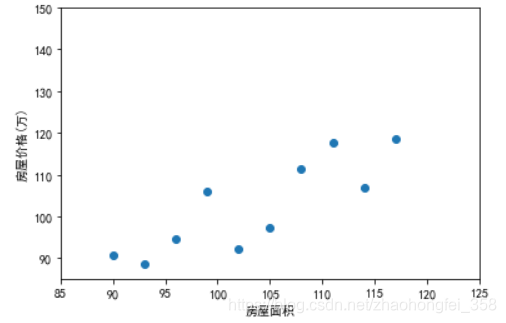
横坐标为房屋面积，纵坐标为房屋价格。根据该图，我们大致可以看出，房屋价格和房屋面积是成线性增长的。

此时，我们就可以绘制出一条直线：

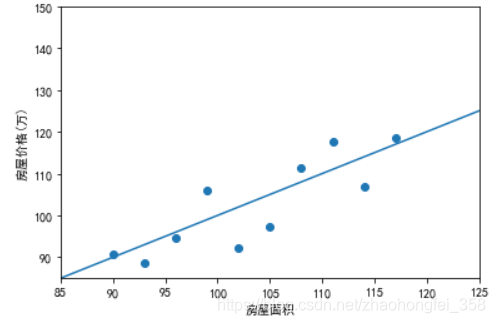
通过这条直线，我们就可以大概预测出，125平的房价是多少了。我们画这条线的依据为：尽可能让每个点回归到这条直线上。

这就是线性回归。而机器学习学的就是如何绘制出这条直线

2. 简单线性回归

上面的例子中，我们的特征只有一个（房屋面积），这样我们就可以在二维平面中观察，如果是两个特征，就需要在三维平面观察。如果超过2个特征，就没办观察了。对于这种只有一个特征的线性回归问题，称为简单线性回归。相应的，高纬的称为多元线性回归。

首先，要熟悉一下相应的数学符号为：

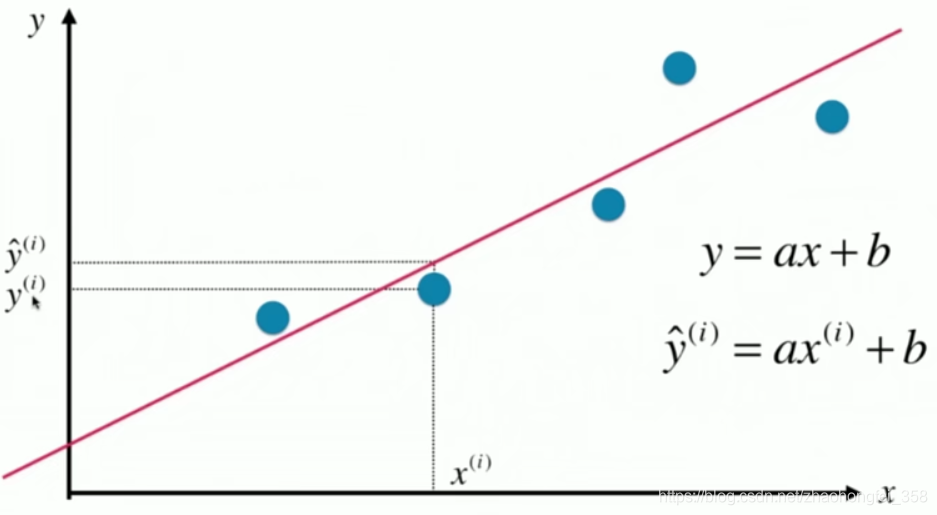
预测的直线，使用 $y=ax+b$ 表示。预测值使用 $\hat{y}^{(i)}$ 表示，读作y hat。$i$ 表示这是第 $i$ 个数据。对于 $x^{(i)}$ 对应的真值，使用 $y^{(i)}$ 表示。

要预测出该线性方程，本质是要预测出 $a$ 和 $b$ 的值。 公式如下：

\begin{aligned} & a = \frac{\sum_{i=1}^m (x^{(i)} - \bar{x})(y^{(i)} - \bar{y})}{\sum_{i=1}^m (x^{(i)} - \bar{x})^2} \\ \\ \\ & b = \bar{y} - a \bar{x} \end{aligned}

其中，$m$ 为样本数量，$x^{(i)}$ 为第 $i$ 个样本的特征值。 $\bar{x}$ 和 $\bar{y}$ 横纵坐标的平均值

2.1 如何预测线性回归方程呢？

思路为：找出一条直线，使得每个点的真值与预测值之间的距离之和最小

假设最佳拟合的直线方程为： $$ \begin{aligned} y=ax+b \end{aligned}$$

则对于每一个样本 $x^{(i)}$ ，它的预测值 $\hat{y}^{(i)}$ 为 $$ \begin{aligned} \hat{y}^{(i)} = a x^{(i)} + b \end{aligned}$$

那该预测值和真值之间的距离则为： $$ \begin{aligned} y^{(i)} - \hat{y}^{(i)} \end{aligned}$$ 为了消除负号，且便于求导，对其进行平方： $$ \begin{aligned} (y^{(i)} - \hat{y}^{(i)})^2 \end{aligned}$$

对所有n个样本样本进行求和，则为： $$ \begin{aligned} \sum_{i=1}^m (y^{(i)} - \hat{y}^{(i)})^2 \end{aligned}$$

其中 $\hat{y}^{(i)} = ax^{(i)} + b$ ，将其带入上式，得： $$ \begin{aligned} f(a,b) = \sum_{i=1}^m (y^{(i)} - ax^{(i)} - b)^2 \end{aligned}$$

我们的目标是，让上式尽可能的小。对于这种使其尽可能小，最终推理出参数的函数，称为损失函数（loss function）

2.1.1 $b$ 的推导过程

我们知道，当 $f'(x) = 0，f''(x) > 0$ ， 函数取极小值。简单起见，我们首先来求 $b$，注意，此时 $b$ 为未知数，所以其他都是常数，所以求导也是对 b 求： \begin{aligned} & f(b) = \sum_{i=1}^m (y^{(i)} - ax^{(i)} - b)^2 \\\\ & f'(b) = (-2)\sum_{i=1}^m (y^{(i)} - ax^{(i)} - b) \\\\ & f''(b) = 2m > 0 \\\\ \end{aligned}

令 f'(b) = 0 ，得 \begin{aligned} & (-2)\sum_{i=1}^m (y^{(i)} - ax^{(i)} - b) = 0 \\\\ & m\cdot b = \sum_{i=1}^m y^{(i)} - a\sum_{i=1}^m x^{(i)} \\\\ & b = \bar{y} - a \bar{x} \end{aligned}

又因为 $f''(b) > 0$，所以当 $b = \bar{y} - a \bar{x}$ 时，$f(b)$ 取最小值

2.1.2 $a$ 的推导过程

与b类似，稍显复杂：

\begin{aligned} & f(a) = \sum_{i=1}^m (y^{(i)} - ax^{(i)} - b)^2 \\\\ & f'(a) = -2\sum_{i=1}^m x^{(i)}(y^{(i)} - ax^{(i)} - b) \\\\ & f''(a) = 2\sum_{i=1}^m (x^{(i)})^2 > 0 \end{aligned}

令 $f'(a) = 0$ ，得： \begin{aligned} -2\sum_{i=1}^m x^{(i)}(y^{(i)} - ax^{(i)} - b) = 0 \\ \\ \sum_{i=1}^m x^{(i)}(y^{(i)} - ax^{(i)} - b) = 0 \end{aligned}

其中 $b = \bar{y} - a \bar{x}$ ，将 $b$ 代入上式，得： \begin{aligned} \sum_{i=1}^m x^{(i)}(y^{(i)} - ax^{(i)} - \bar{y} + a \bar{x}) & = 0 \\\\ \sum_{i=1}^m x^{(i)}y^{(i)} - \sum_{i=1}^ma(x^{(i)})^2 - \sum_{i=1}^m x^{(i)}\bar{y} + \sum_{i=1}^ma x^{(i)}\bar{x} & = 0 \\\\ a\sum_{i=1}^m((x^{(i)})^2 - x^{(i)}\bar{x}) &= \sum_{i=1}^m(x^{(i)}y^{(i)} - \bar{y}x^{(i)}) \\\\ \end{aligned}

将左边除过去，得 $a$ ： $$ \begin{aligned} a = \frac{ \sum_{i=1}^m(x^{(i)}y^{(i)} - \bar{y}x^{(i)})}{\sum_{i=1}^m((x^{(i)})^2 - x^{(i)}\bar{x})} \end{aligned}$$

此时，我们就得到 $a$ ，但为了方便进行向量化运算（可以方便使用numpy加快运行速度），对该式继续改造。

已知： \begin{aligned} \sum_{i=1}^m x^{(i)} \bar{y} = \bar{y}\sum_{i=1}^m x^{(i)} &= m\bar{y}\cdot\bar{x} = \bar{x}\sum_{i=1}^m y^{(i)} = \sum_{i=1}^m y^{(i)} \bar{x} \\ &=\sum_{i=1}^m \bar{x}\cdot\bar{y} \end{aligned}

根据上式，继续对a进行处理，可得： \begin{aligned} a = \frac{ \sum_{i=1}^m(x^{(i)}y^{(i)} - \bar{y}x^{(i)} - \bar{x}y^{(i)} + \bar{x}\bar{y})}{\sum_{i=1}^m((x^{(i)})^2 - x^{(i)}\bar{x} - x^{(i)}\bar{x} + (\bar{x})^2)} \\ \\ a = \frac{\sum_{i=1}^m(x^{(i)} - \bar{x})(y^{(i)} - \bar{y})}{\sum_{i=1}^m (x^{(i) }- \bar{x})^2} \end{aligned}

此时，上底下底都转成了 $$ \begin{aligned} y = w\cdot v \end{aligned}$$

就可以方便的进行向量运算了

3. 线性回归评测

当模型训练好后，需要对模型的好坏进行评测。我们需要使用训练测试集进行评测，通常有以下几种方式：

3.1 均方误差（MSE，Mean Squared Error）

$$ \begin{aligned} MSE = \frac{1}{m} \sum^{m}_{i=1} (y^{(i)}_{test}-\hat{y}^{(i)}_{test})^2 \end{aligned}$$ 其中 $y^{(i)}_{test}$ 为测试数据的 $y$ 值，$\hat{y}^{(i)}_{test}$ 为预测结果。对它们的差平方后求和，再除以样本数量 $m$

该方法使用的方差的思想，缺点是结果和误差量岗不一致。

3.2 均方根误差（RMSE，Root Mean Squared Error）

$$ \begin{aligned} RMSE = \sqrt{MSE} = \sqrt{\frac{1}{m} \sum^{m}_{i=1} (y^{(i)}_{test}-\hat{y}^{(i)}_{test})^2} \end{aligned}$$

为了解决均方误差量岗不一致的缺点，使用标准差的思想，对其进行开方，就可以保证量岗一致了。

3.3 平均绝对误差（MAE，Mean Absolute Error）

$$ \begin{aligned} MAE = \frac{1}{m} \sum^{m}_{i=1} |y^{(i)}_{test}-\hat{y}^{(i)}_{test}| \end{aligned}$$

该方法很直白，直接计算距离求和，然后求平均。这样就很方便的保证了量岗

3.3.1 RMSE 和 MAE 比较

RMSE和MAE都可以求误差，但是，学方差的时候我们知道，开方是为了增大误差较大的数据的影响，所以往往RMSE的值要比MAE的值大。在实践中，使RMSE的值尽可能的小会更有意义。

3.4 R Squared

问题提出：还记得相对标准偏差么。当预测的多个模型单位不一致时，例如我预测出的房价RMSE误差为1万元，你预测出的考试成绩RMSE为10分，那么这样是很难比较说明谁的模型更好。

此时聪明的科学家就提出了 R Squared ：

\begin{aligned} R^2 & = 1 - \frac{SS_{residual}}{SS_{total}} \\\\ & = 1 - \frac{\sum^{m}_{i=1} (\hat{y}^{(i)} - y^{(i)}) ^ 2}{\sum^{m}_{i=1} (\bar{y} - y^{(i)})^ 2} \end{aligned}

其中，分子 $SS_{residual}$ (Residual Sum of Squares) 表示预测值与真值误差平方之和，分母 $SS_{total}$ (Total Sum of Squares) 表示平均值与真值误差平方之和。

换言之，减号右边就是想看看用预测出的模型的误差 和 直接用平均值作为模型的误差 进行比较，看看其效果怎么样（平均值被称为基准模型（Baseline Model））。所以就可以得出以下结论：

1. $R^2<=1$ 。因为减号右边一定大于0
2. $R^2$ 越大越好。当预测结果与实际结果完全一致时，分子 $SS_{residual}=0$，所以 $R^2=1$。
3. $R^2$ 越小越坏。当预测模型和基准模型效果差不多时，$R^2=0$。当 $R^2 <0$ 时，说明预测模型还不如基准模型，此时，数据很有可能不存在线性关系

我们现在对 R Squared 再做一下改造：

\begin{aligned} R^2 &= 1 - \frac{\sum^{m}_{i=1} (\hat{y}^{(i)} - y^{(i)}) ^ 2}{\sum^{m}_{i=1} (\bar{y} - y^{(i)})^ 2} \\\\ &= 1 - \frac{(\sum^{m}_{i=1} (\hat{y}^{(i)} - y^{(i)}) ^ 2)/m}{(\sum^{m}_{i=1} (\bar{y} - y^{(i)})^ 2)/m} \\\\ & = 1- \frac{MSE(\hat{y},y)}{Var(y)} \end{aligned}

其中，$MSE(\hat{y},y)$为模型的均方误差，$Var(y)$ 为数据方差。使用该公式，可以更方便编码。

4. 多元线性回归

特征数为1时，可以在2维平面中观察，为2时，可以在3维平面中观察。超过了2，就无法观察了。对于特征数超过1的线性回归方程，称为多元线性回归。

当我们只有一个特征时，线性方程为： $$ \begin{aligned} y = \theta_0 + \theta_1 x_1 ~~~~~（y=ax + b） \end{aligned}$$

当有两个特征时，线性方程为： $$ \begin{aligned} y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 \end{aligned}$$

以此类推，当有n个特征时，线性方程为： $$ \begin{aligned} y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n \end{aligned}$$

所以，我们构建模型就是算出 $\theta_0, \theta_1, \cdots \theta_n$ 的值

当推算出 $\theta_0, \theta_1, \cdots \theta_n$ 后，就可以预测 $\hat{y}$ 了，： $$ \begin{aligned} \hat{y}^{(i)} = \theta_0 + \theta_1 X_1^{(i)} + \theta_2 X_2^{(i)} + \cdots + \theta_n X_n^{(i)} \end{aligned}$$

其中，$\hat{y}$ 是预测出的值，$X_1, X_2, \cdots, X_n$ 是输入数据的n个特征

同样，多元线性回归的目标也是使 $\sum_{i=1}^m (y^{(i)} - \hat{y}^{(i)})^2$ 尽可能小。

我们可以将 $\hat{y}^{(i)}$ 写成向量形式：

$$ \begin{aligned} \hat{y}^{(i)} = X^{(i)} \cdot \theta ~~~~其中 \theta=(\theta_0,\theta_1, \cdots , \theta_n)^T , X^{(i)} = (1, X_1^{(i)},X_2^{(i)}, \cdots, X_n^{(i)}) \end{aligned}$$

对于整个 $\hat{y}$，表示成向量，即为： $$ \begin{aligned} \hat{y} = X_b \cdot \theta \\\\ \end{aligned}$$

其中： \begin{aligned} X_b = \begin{pmatrix} 1 & X_1^{(1)} & X_2^{(1)} & \dots X_n^{(1)} \\\\ 1 & X_1^{(2)} & X_2^{(2)} & \dots X_n^{(2)} \\\\ \cdots & & & \cdots \\\\ 1 & X_1^{(m)} & X_2^{(m)} & \dots X_n^{(m)} \\ \end{pmatrix}~~~~~~~~~~ \theta= \begin{pmatrix} \theta_0\\\\ \theta_1\\\\ \theta_2\\\\ \cdots \\\\ \theta_n\\\\ \end{pmatrix} \end{aligned}

根据线性代数知识，我们知道： $$ \begin{aligned} \sum^{m}_{i=1} x_i^2 = x_1^2 + x_2^2 + \cdots + x_n^2 = (x_1, x_2, \cdots, x_n) \cdot (x_1, x_2, \cdots, x_n)^T = X^T \cdot X \\\\ 其中 X = (x_1,x_2, \cdots, x_n)^T \end{aligned}$$

所以，根据上面两个式子，对 $\sum_{i=1}^m (y^{(i)} - \hat{y}^{(i)})^2$ 进行向量化处理，可得： $$ \begin{aligned} \sum_{i=1}^m (y^{(i)} - \hat{y}^{(i)})^2 = (y-X_b \cdot \theta)^T(y-X_b \cdot \theta) \end{aligned}$$

经过推导（推导过程），可以推出 $\theta$，得： $$ \begin{aligned} \theta = (X_b^T X_b)^{-1} X_b^T y \end{aligned}$$

该式子称为多元线性回归的正规方程解（Normal Equation）

• 缺点：时间复杂度高 O(n^3^)，即使优化后，也有 O(n^2.4^)
• 优点：不需要对数据做归一化处理

5. 线性回归方程的可解释性

例如，我们对于房价预测，得到了以下数据： $$ \begin{aligned} \theta= \begin{pmatrix} \theta_0 \\\\ \theta_1\\\\ \theta_2\\\\ \theta_3 \\\\ \theta_4\\\\ \end{pmatrix} = \begin{pmatrix} -1.3 \\\\ -2.5\\\\ 0 \\\\ 7.5 \\\\ 3 \\\\ \end{pmatrix} \to \begin{pmatrix} 空气污染程度 \\\\ 周边工厂数量\\\\ 小区大门数量 \\\\ 房屋面积 \\\\ 小区绿化程度 \\\\ \end{pmatrix} \end{aligned}$$

可以看到，该数据中有正有负，其中正数就代表该特征与结果呈正相关，例如房屋面积越大，房价越高。负数则说明该特征与结果呈负相关，例如周边工厂数量越多，房价越低。

而系数的大小说明了该特征对结果的影响大小，系数的绝对值越大，说明该特征对结果影响越大，例如周边工厂的数量相比空气污染程度对房价的影响更大。

这就是线性回归方程的可解释性，我们可以通过线性回归方程看出得到一些结论。所以，及时拿到数据之后，不知道用哪一种算法进行预测，也可以先使用线性回归试一下，至少能看出这些特征对结果的影响程度

---

参考资料

第五章 线性回归法: https://coding.imooc.com/class/chapter/169.html

多元线性回归方程正规方程解（Normal Equation）公式推导详细过程: https://blog.csdn.net/zhaohongfei_358/article/details/118678245

考研必备数学公式大全: https://blog.csdn.net/zhaohongfei_358/article/details/106039576